Mexico
United Mexican States Estados Unidos Mexicanos (Spanish) | |
|---|---|
| Anthem: "Himno Nacional Mexicano" ("Mexican National Anthem") | |
| Capital and largest city | Mexico City 19°26′N 99°8′W / 19.433°N 99.133°W |
| Official languages | Spanish (de facto) |
| Co-official languages | |
| Ethnic groups | See below |
| Religion (2023)[1] |
|
| Demonym(s) | Mexican |
| Government | Federal presidential republic[2] |
| Andrés Manuel López Obrador | |
| Ana Lilia Rivera | |
| Marcela Guerra Castillo | |
| Norma Lucía Piña Hernández | |
| Legislature | Congress |
| Senate | |
| Chamber of Deputies | |
| Independence from Spain | |
| 16 September 1810 | |
• Declared | 27 September 1821 |
| 28 December 1836 | |
| 4 October 1824 | |
| 5 February 1857 | |
| 5 February 1917 | |
| Area | |
• Total | 1,972,550 km2 (761,610 sq mi) (13th) |
• Water (%) | 1.58 (as of 2015)[3] |
| Population | |
• 2023 estimate | |
• Density | 61/km2 (158.0/sq mi) (142nd) |
| GDP (PPP) | 2024 estimate |
• Total | |
• Per capita | |
| GDP (nominal) | 2024 estimate |
• Total | |
• Per capita | |
| Gini (2018) | medium |
| HDI (2022) | high (77th) |
| Currency | Mexican peso (MXN) |
| Time zone | UTC−8 to −5 (See Time in Mexico) |
• Summer (DST) | UTC−7 to −5 (varies) |
| Date format | dd/mm/yyyy |
| Driving side | right |
| Calling code | +52 |
| ISO 3166 code | MX |
| Internet TLD | .mx |
Mexico,[a][b] officially the United Mexican States,[c] is a country in the southern portion of North America. Covering 1,972,550 km2 (761,610 sq mi),[11] it is the world's 13th largest country by area; with a population of almost 130 million, it is the 10th most populous country and has the most Spanish speakers in the world.[12] Mexico is organized as a federal constitutional republic comprising 31 states and Mexico City, its capital and largest city, which is among the world's most populous metropolitan areas. The country shares land borders with the United States to the north, with Guatemala and Belize to the southeast; as well as maritime borders with the Pacific Ocean to the west, the Caribbean Sea to the southeast, and the Gulf of Mexico to the east.[13]
Human presence in Pre-Columbian Mexico dates back to 8,000 BC, making it one of the world's six cradles of civilization. The Mesoamerican region hosted various intertwined civilizations, including the Olmec, Maya, Zapotec, Teotihuacan, and Purepecha. The Aztecs came to dominate the area prior to European contact. In 1521, the Spanish Empire, alongside indigenous allies, conquered the Aztec Empire, establishing the colony of New Spain centered in the former capital, Tenochtitlan (now Mexico City).[14] Over the next three centuries, Spain expanded its territorial control, enforced Christianity, and spread the Spanish language, with the colony's rich silver deposits fueling its empire.[15] The colonial era ended in the early 19th century with the Mexican War of Independence.
Following independence, Mexico faced political and socioeconomic upheaval. The United States' invasion during the Mexican–American War resulted in significant territorial losses in 1848.[16] Liberal reforms introduced in the Constitution of 1857 prompted domestic conflict, French intervention, and the establishment of an Empire, countered by the Republican resistance led by Benito Juárez. The late 19th century saw the rise of Porfirio Díaz's dictatorship,[17] sparking the Mexican Revolution in 1910, which led to profound changes, including the 1917 Constitution. A succession of presidents, often former generals, persisted until the emergence of the Institutional Revolutionary Party (PRI) in 1929. Over the next 70 years of PRI rule, Mexico experienced significant economic growth, but also faced issues of repression and electoral fraud. The late twentieth century saw a shift towards neoliberal policies, exemplified by the signing of the North American Free Trade Agreement (NAFTA) in 1994, amidst social unrest and indigenous rebellion in Chiapas. In 2000, the PRI lost the presidency for the first time to the conservative National Action Party (PAN).
Mexico is a newly industrialized and developing country,[18] with the world's 12th-largest economy by nominal GDP and 12th-largest by PPP; the United States is its largest economic partner. Mexico ranks first in the Americas and seventh in the world by the number of UNESCO World Heritage Sites.[19] It is also one of the world's 17 megadiverse countries, ranking fifth in natural biodiversity.[20] Mexico's rich cultural and biological heritage, as well as varied climate and geography, makes it a major tourist destination: as of 2022, it is the sixth most-visited country in the world, with 42.2 million international arrivals.[21] Mexico's large economy and population, global cultural influence (particularly in cuisine, media, and art), and steady democratization make it a regional and middle power,[22][23][24] and it is increasingly identified as an emerging power by several analysts.[25][26][27][28]
Although Mexico has made significant political and socioeconomic gains in recent decades, ranking 77th in the Human Development Index, it continues to struggle with social inequality, poverty, systemic corruption, and extensive crime.[29] Since 2006, an ongoing conflict between drug trafficking syndicates has led to over 120,000 deaths.[30][needs update] Mexico is a member of United Nations, the G20, the Organisation for Economic Co-operation and Development (OECD), the World Trade Organization (WTO), the Asia-Pacific Economic Cooperation forum, the Organization of American States, Community of Latin American and Caribbean States, and the Organization of Ibero-American States.
Etymology
Mēxihco is the Nahuatl term for the heartland of the Aztec Empire, namely the Valley of Mexico and surrounding territories, with its people being known as the Mexica. It is generally believed that the toponym for the valley was the origin of the primary ethnonym for the Aztec Triple Alliance, but it may have been the other way around.[31] In the colonial era (1521–1821) Mexico was known as New Spain. In the eighteenth century, this central region became the Intendency of Mexico, during the reorganization of the empire, the Bourbon Reforms. After New Spain achieved independence from the Spanish Empire in 1821 and became a sovereign state, the territory came to be known as the State of Mexico, with the new country being named after its capital: Mexico City. The country's official name has changed as the form of government has changed. The declaration of independence signed on 6 November 1813 by the deputies of the Congress of Anáhuac called the territory América Septentrional (Northern America); the 1821 Plan of Iguala also used América Septentrional. On two occasions (1821–1823 and 1863–1867), the country was known as Imperio Mexicano (Mexican Empire). All three federal constitutions (1824, 1857, and 1917, the current constitution) used the name Estados Unidos Mexicanos[32]—or the variant Estados-Unidos Mexicanos,[33] all of which have been translated as "United Mexican States". The phrase República Mexicana, "Mexican Republic", was used in the 1836 Constitutional Laws.[34]
History
Indigenous civilizations before European contact (pre-1519)



The earliest human artifacts in Mexico are chips of stone tools found near campfire remains in the Valley of Mexico and radiocarbon-dated to circa 10,000 years ago.[35] Mexico is the site of the domestication of maize, tomato, and beans, which produced an agricultural surplus. This enabled the transition from paleo-Indian hunter-gatherers to sedentary agricultural villages beginning around 5000 BC.[36] In the subsequent formative eras, maize cultivation and cultural traits such as a mythological and religious complex, and a vigesimal (base 20) numeric system, were diffused from the Mexican cultures to the rest of the Mesoamerican culture area.[37] In this period, villages became more dense in terms of population, becoming socially stratified with an artisan class, and developing into chiefdoms. The most powerful rulers had religious and political power, organizing the construction of large ceremonial centers.[38]
The earliest complex civilization in Mexico was the Olmec culture, which flourished on the Gulf Coast from around 1500 BC. Olmec cultural traits diffused through Mexico into other formative-era cultures in Chiapas, Oaxaca, and the Valley of Mexico. The formative period saw the spread of distinct religious and symbolic traditions, as well as artistic and architectural complexes.[39] The formative-era of Mesoamerica is considered one of the six independent cradles of civilization. In the subsequent pre-classical period, the Maya and Zapotec civilizations developed complex centers at Calakmul and Monte Albán, respectively. During this period the first true Mesoamerican writing systems were developed in the Epi-Olmec and Zapotec cultures. The Mesoamerican writing tradition reached its height in the Classic Maya Hieroglyphic script. The earliest written histories date from this era. The tradition of writing was important after the Spanish conquest in 1521, with indigenous scribes learning to write their languages in alphabetic letters, while also continuing to create pictorial texts.[40][41]
In Central Mexico, the height of the classic period saw the ascendancy of Teotihuacán, which formed a military and commercial empire. Teotihuacan, with a population of more than 150,000 people, had some of the largest pyramidal structures in the pre-Columbian Americas.[42] After the collapse of Teotihuacán around 600 AD, competition ensued between several important political centers in central Mexico such as Xochicalco and Cholula. At this time, during the Epi-Classic, Nahua peoples began moving south into Mesoamerica from the North, and became politically and culturally dominant in central Mexico, as they displaced speakers of Oto-Manguean languages. During the early post-classic era (ca. 1000–1519 AD), Central Mexico was dominated by the Toltec culture, Oaxaca by the Mixtec, and the lowland Maya area had important centers at Chichén Itzá and Mayapán. Toward the end of the post-Classic period, the Mexica established dominance, establishing a political and economic empire based in the city of Tenochtitlan (modern Mexico City), extending from central Mexico to the border with Guatemala.[43] Alexander von Humboldt popularized the modern usage of "Aztec" as a collective term applied to all the people linked by trade, custom, religion, and language to the Mexica state and Ēxcān Tlahtōlōyān, the Triple Alliance.[44] In 1843, with the publication of the work of William H. Prescott, it was adopted by most of the world. This usage has been the subject of debate since the late 20th century.[45]
Spanish conquest and colonial era (1519–1821)

Although the Spanish Empire had established colonies in the Caribbean starting in 1493, only in the second decade of the sixteenth century did they begin exploring the east coast of Mexico. The Spanish first learned of Mexico during the Juan de Grijalva expedition of 1518. The Spanish conquest of the Aztec Empire began in February 1519 when Hernán Cortés founded the Spanish city of Veracruz. The 1521 capture of Tenochtitlan and immediate founding of the Spanish capital Mexico City on its ruins was the beginning of a 300-year-long colonial era during which Mexico was known as Nueva España (New Spain). Two factors made Mexico a jewel in the Spanish Empire: the existence of large, hierarchically organized Mesoamerican populations that rendered tribute and performed obligatory labor and the discovery of vast silver deposits in northern Mexico.[46]

The Kingdom of New Spain was created from the remnants of the Aztec empire. The two pillars of Spanish rule were the State and the Roman Catholic Church, both under the authority of the Spanish crown. In 1493 the pope had granted sweeping powers to the Spanish monarchy for its overseas empire, with the proviso that the crown spread Christianity in its new realms. In 1524, King Charles I created the Council of the Indies based in Spain to oversee State power in its overseas territories; in New Spain the crown established a high court in Mexico City, the Real Audiencia ('royal audience' or 'royal tribunal'), and then in 1535 created the Viceroyalty of New Spain. The viceroy was the highest official of the State. In the religious sphere, the Diocese of Mexico was created in 1530 and elevated to the Archdiocese of Mexico in 1546, with the archbishop as the head of the ecclesiastical hierarchy. Castilian Spanish was the language of rulers. The Catholic faith was the only one permitted, with non-Catholics and Catholics (excluding Indians) holding unorthodox views being subject to the Mexican Inquisition, established in 1571.[47]

Spanish military forces, sometimes accompanied by native allies, led expeditions to conquer territory or quell rebellions through the colonial era. Notable Amerindian revolts in sporadically populated northern New Spain include the Chichimeca War (1576–1606),[48] Tepehuán Revolt (1616–1620),[49] and the Pueblo Revolt (1680), the Tzeltal Rebellion of 1712 was a regional Maya revolt.[50] Most rebellions were small-scale and local, posing no major threat to the ruling elites.[51] To protect Mexico from the attacks of English, French, and Dutch pirates and protect the Crown's monopoly of revenue, only two ports were open to foreign trade—Veracruz on the Atlantic (connecting to Spain) and Acapulco on the Pacific (connecting to the Philippines). Among the best-known pirate attacks are the 1663 Sack of Campeche[52] and 1683 Attack on Veracruz.[53] Of greater concern to the crown was the issue of foreign invasion, especially after Britain seized in 1762 the Spanish ports of Havana and Manila in the Seven Years' War. It created a standing military, increased coastal fortifications, and expanded the northern presidios and missions into Alta California. The volatility of the urban poor in Mexico City was evident in the 1692 riot in the Zócalo. The riot over the price of maize escalated to a full-scale attack on the seats of power, with the viceregal palace and the archbishop's residence attacked by the mob.[54]
Independence era (1808–1855)

The upheaval in the Spanish Empire that resulted in the independence of most of its New World territories was due to Napoleon Bonaparte's invasion of Spain in 1808. In Mexico, elites argued that sovereignty now reverted to "the people" and that town councils (cabildos) were the most representative bodies.[55] On 16 September 1810, secular priest Miguel Hidalgo y Costilla declared against "bad government" in the small town of Dolores, Guanajuato. This event, known as the Cry of Dolores (Spanish: Grito de Dolores) is commemorated each year, on 16 September, as Mexico's independence day.[56] Hidalgo and some of his soldiers were eventually captured, Hidalgo was defrocked, and they were executed by firing squad on 31 July 1811.


The first 35 years after Mexico's independence were marked by political instability and the changing of the Mexican state from a transient monarchy to a fragile federated republic.[57] There were military coups d'état, foreign invasions, ideological conflict between Conservatives and Liberals, and economic stagnation. Catholicism remained the only permitted religious faith and the Catholic Church as an institution retained its special privileges, prestige, and property, a bulwark of Conservatism. The army, another Conservative-dominated institution, also retained its privileges. Former Royal Army General Agustín de Iturbide became regent, as newly independent Mexico sought a constitutional monarch from Europe. When no member of a European royal house desired the position, Iturbide himself was declared Emperor Agustín I. The United States was the first country to recognize Mexico's independence, sending an ambassador to the court and sending a message to Europe via the Monroe Doctrine not to intervene in Mexico. The emperor's rule was short (1822–1823) and he was overthrown by army officers in the Plan of Casa Mata.[58]
After the forced abdication of the monarch, Central America and Chiapas left the union to form the Federal Republic of Central America. In 1824, a constitution of a federated republic was promulgated and the First Mexican Republic was established. Former insurgent General Guadalupe Victoria became the first president of the republic — the first of many army generals to hold the presidency.
In 1829, former insurgent general and fierce Liberal Vicente Guerrero, a signatory of the Plan of Iguala that achieved independence, became president in a disputed election. During his short term in office, from April to December 1829, he abolished slavery. As a visibly mixed-race man of modest origins, Guerrero was seen by white political elites as an interloper.[59] His Conservative vice president, former Royalist General Anastasio Bustamante, led a coup against him and Guerrero was judicially murdered.[60] There was constant strife between the Liberals (also known as Federalists), who were supporters of a federal form of decentralized government, and their political rivals, the Conservatives (also known as Centralists), who proposed a hierarchical form of government.
Mexico's ability to maintain its independence and establish a viable government was in question. Spain attempted to reconquer its former colony during the 1820s but eventually recognized its independence. France attempted to recoup losses it claimed for its citizens during Mexico's unrest and blockaded the Gulf Coast during the so-called Pastry War of 1838–1839.[61] General Antonio López de Santa Anna emerged as a national hero because of his role in both these conflicts; Santa Anna came to dominate the politics for the next 25 years, often known as the "Age of Santa Anna", until his overthrow in 1855.[62]

Mexico also contended with indigenous groups that controlled the territory that Mexico claimed in the north. For example, the Comanche controlled a huge territory in sparsely populated central and northern Texas.[63] Wanting to stabilize and develop that area — and as few people from central Mexico had chosen to resettle to this remote and hostile territory — the Mexican government encouraged Anglo-American immigration into present-day Texas, a region that bordered that United States. Mexico by law was a Catholic country; the Anglo-Americans were primarily Protestant English speakers from the southern United States. Some brought their black slaves, which after 1829 was contrary to Mexican law. In 1835, Santa Anna sought to centralize government rule in Mexico, suspending the 1824 constitution and promulgating the Seven Laws, which placed power in his hands. As a result, civil war spread across the country. Three new governments declared independence: the Republic of Texas, the Republic of the Rio Grande and the Republic of Yucatán.[64]: 129–137 The largest blow to Mexico was the U.S. invasion of Mexico in 1846 in the Mexican–American War. Mexico lost much of its sparsely populated northern territory, sealed in the 1848 Treaty of Guadalupe Hidalgo. Despite that disastrous loss, Santa Anna returned to the presidency yet again before being ousted and exiled in the Liberal Revolution of Ayutla.
Liberal era (1855–1911)

The overthrow of Santa Anna and the establishment of a civilian government by Liberals allowed them to enact laws that they considered vital for Mexico's economic development. The Liberal Reform attempted to modernize Mexico's economy and institutions along liberal principles. They promulgated a new Constitution of 1857, separating Church and State, stripping the Church and the military of their special privileges (fueros); mandating the sale of Church-owned property and sale of indigenous community lands, and secularizing education.[65] Conservatives revolted, touching off civil war between rival Liberal and Conservative governments (1858–1861).
The Liberals defeated the Conservative army on the battlefield, but Conservatives sought another solution to gain power via foreign intervention by the French. Mexican conservatives asked Emperor Napoleon III to place a European monarch as head of state in Mexico. The French Army defeated the Mexican Army and placed Maximilian Habsburg on the newly established throne of Mexico, supported by Mexican Conservatives and propped up by the French Army. The Liberal Republic under Benito Juárez was a government in internal exile, but with the end of the Civil War in the U.S. in April 1865, that government began aiding the Mexican Republic. Two years later, the French Army withdrew its support, but Maximilian remained in Mexico. Republican forces captured him and he was executed. The "Restored Republic" saw the return of Juárez, "the personification of the embattled republic,"[66] as president.
The Conservatives had been not only defeated militarily but also discredited politically for their collaboration with the French invaders. Liberalism became synonymous with patriotism.[67] The Mexican Army that had its roots in the colonial royal army and then the army of the early republic was destroyed. New military leaders had emerged from the War of the Reform and the conflict with the French, most notably Porfirio Díaz, a hero of the Cinco de Mayo, who now sought civilian power. Juárez won re-election in 1867 but was challenged by Díaz. Díaz then rebelled, crushed by Juárez. Having won re-election, Juárez died in office in July 1872, and Liberal Sebastián Lerdo de Tejada became president, declaring a "religion of the state" for the rule of law, peace, and order. When Lerdo ran for re-election, Díaz rebelled against the civilian president, issuing the Plan of Tuxtepec. Díaz had more support and waged guerrilla warfare against Lerdo. On the verge of Díaz's victory on the battlefield, Lerdo fled from office into exile.[68]

After the turmoil in Mexico from 1810 to 1876, the 35-year rule of Liberal General Porfirio Díaz (r.1876–1911) allowed Mexico to rapidly modernize in a period characterized as one of "order and progress". The Porfiriato was characterized by economic stability and growth, significant foreign investment and influence, an expansion of the railroad network and telecommunications, and investments in the arts and sciences.[69]
Díaz ruled with a group of advisors that became known as the científicos ('scientists').[70] The most influential científico was Secretary of Finance José Yves Limantour.[71] The Porfirian regime was influenced by positivism.[72] They rejected theology and idealism in favor of scientific methods being applied towards national development. An integral aspect of the liberal project was secular education. The Díaz government led a protracted conflict against the Yaqui that culminated with the forced relocation of thousands of Yaqui to Yucatán and Oaxaca. As the centennial of independence approached, Díaz gave an interview where he said he was not going to run in the 1910 elections, when he would be 80. Political opposition had been suppressed and there were few avenues for a new generation of leaders. But his announcement set off a frenzy of political activity, including the unlikely candidacy of the scion of a rich landowning family, Francisco I. Madero. Madero won a surprising amount of political support when Díaz changed his mind and ran in the election, jailing Madero. The September centennial celebration of independence was the last celebration of the Porfiriato. The Mexican Revolution starting in 1910 saw a decade of civil war, the "wind that swept Mexico."[73]
Mexican Revolution (1910–1920)

The Mexican Revolution was a decade-long transformational conflict.[74] It began with scattered uprisings against President Díaz after the fraudulent 1910 election, his resignation in May 1911, demobilization of rebel forces and an interim presidency of a member of the old guard, and the democratic election of a rich, civilian landowner, Francisco I. Madero in fall 1911. In February 1913, a military coup d'état overthrew Madero's government, with the support of the U.S., resulting in Madero's murder by agents of Federal Army General Victoriano Huerta. A coalition of anti-Huerta forces in the North, the Constitutional Army led by Governor of Coahuila Venustiano Carranza, and a peasant army in the South under Emiliano Zapata defeated the Federal Army.[75]
In 1914, that army was dissolved as an institution, leaving only revolutionary forces. Following the revolutionaries' victory against Huerta, they sought to broker a peaceful political solution, but the coalition splintered, plunging Mexico again into a civil war. Constitutionalist general Pancho Villa, commander of the Division of the North, broke with Carranza and allied with Zapata. Carranza's best general Alvaro Obregón defeated Villa, his former comrade-in-arms in the Battle of Celaya in 1915, and Villa's northern forces melted away. Zapata's forces in the south reverted to guerrilla warfare. Carranza became the de facto head of Mexico, and the U.S. recognized his government.[75]
In 1916, the winners met at a constitutional convention to draft the Constitution of 1917, which was ratified in February 1917. The Constitution empowered the government to expropriate resources including land, gave rights to labor, and strengthened anticlerical provisions of the 1857 Constitution.[75] With amendments, it remains the governing document of Mexico. It is estimated that the war killed 900,000 of the 1910 population of 15 million.[76][77] Although often viewed as an internal conflict, the revolution had significant international elements.[78] During the Revolution, the U.S. Republican administration of Taft supported the Huerta coup against Madero, but when Democrat Woodrow Wilson was inaugurated as president in March 1913, Wilson refused to recognize Huerta's regime and allowed arms sales to the Constitutionalists. Wilson ordered troops to occupy the strategic port of Veracruz in 1914, which was lifted.[79]

After Pancho Villa was defeated by revolutionary forces in 1915, he led an incursion raid into Columbus, New Mexico, prompting the U.S. to send 10,000 troops led by General John J. Pershing in an unsuccessful attempt to capture Villa. Carranza pushed back against U.S. troops being in northern Mexico. The expeditionary forces withdrew as the U.S. entered World War I.[80] Germany attempted to get Mexico to side with it, sending a coded telegram in 1917 to incite war between the U.S. and Mexico, with Mexico to regain the territory it lost in the Mexican-American War.[81] Mexico remained neutral in the conflict.
Consolidating power, President Carranza had peasant leader Emiliano Zapata assassinated in 1919. Carranza had gained the support of the peasantry during the Revolution, but once in power, he did little to institute land reform, which had motivated many to fight in the Revolution. Carranza returned some confiscated land to their original owners. President Carranza's best general, Obregón, served briefly in his administration but returned to his home state of Sonora to position himself to run in the 1920 presidential election. Since Carranza could not run for re-election, he chose a civilian to succeed him, intending to remain the power behind the presidency. Obregón and two other Sonoran revolutionary generals drew up the Plan of Agua Prieta, overthrowing Carranza, who died fleeing Mexico City in 1920. General Adolfo de la Huerta became interim president, followed by the election of General Álvaro Obregón.
Political consolidation and one-party rule (1920–2000)

The first quarter-century of the post-revolutionary period (1920–1946) was characterized by revolutionary generals serving as Presidents of Mexico, including Álvaro Obregón (1920–24), Plutarco Elías Calles (1924–28), Lázaro Cárdenas (1934–40), and Manuel Avila Camacho (1940–46). The post-revolutionary project of the Mexican government sought to bring order to the country, end military intervention in politics, and create organizations of interest groups. Workers, peasants, urban office workers, and even the army for a short period were incorporated as sectors of the single party that dominated Mexican politics from its founding in 1929. Obregón instigated land reform and strengthened the power of organized labor. He gained recognition from the United States and took steps to settle claims with companies and individuals that lost property during the Revolution. He imposed his fellow former Sonoran revolutionary general, Calles, as his successor, prompting an unsuccessful military revolt. As president, Calles provoked a major conflict with the Catholic Church and Catholic guerrilla armies when he strictly enforced anticlerical articles of the 1917 Constitution. The Church-State conflict was mediated and ended with the aid of the U.S. Ambassador to Mexico and ended with an agreement between the parties in conflict. Although the constitution prohibited the reelection of the president, Obregón wished to run again and the constitution was amended to allow non-consecutive re-election. Obregón won the 1928 elections but was assassinated by a Catholic activist, causing a political crisis of succession. Calles could not become president again, since he had just ended his term. He sought to set up a structure to manage presidential succession, founding the party that was to dominate Mexico until the late twentieth century. Calles declared that the Revolution had moved from caudillismo (rule by strongmen) to the era institucional (institutional era).[82]
Despite not holding the presidency, Calles remained the key political figure during the period known as the Maximato (1929–1934). The Maximato ended during the presidency of Lázaro Cárdenas, who expelled Calles from the country and implemented many economic and social reforms. This included the Mexican oil expropriation in March 1938, which nationalized the U.S. and Anglo-Dutch oil company known as the Mexican Eagle Petroleum Company. This movement would result in the creation of the state-owned Mexican oil company Pemex. This sparked a diplomatic crisis with the countries whose citizens had lost businesses by Cárdenas's radical measure, but since then the company has played an important role in the economic development of Mexico. Cárdenas's successor, Manuel Ávila Camacho (1940–1946) was more moderate, and relations between the U.S. and Mexico vastly improved during World War II, when Mexico was a significant ally, providing manpower and materiel to aid the war effort. From 1946 the election of Miguel Alemán, the first civilian president in the post-revolutionary period, Mexico embarked on an aggressive program of economic development, known as the Mexican miracle, which was characterized by industrialization, urbanization, and the increase of inequality in Mexico between urban and rural areas.[83] The Green Revolution, a technological movement that led to a significant worldwide increase in crop production, began in the Yaqui Valley of Sonora in the middle of the 20th century.[84]

With robust economic growth, Mexico sought to showcase it to the world by hosting the 1968 Summer Olympics. The government poured huge resources into building new facilities, prompting political unrest among university students and others. Demonstrations in central Mexico City went on for weeks before the planned opening of the games, with the government of Gustavo Díaz Ordaz cracking down. The culmination was the Tlatelolco Massacre,[85] which killed around 300 protesters based on conservative estimates and perhaps as many as 800.[86] Although the economy continued to flourish for some, social inequality remained a factor of discontent. PRI rule became increasingly authoritarian and at times oppressive in what is now referred to as the Mexican Dirty War.[87]
Luis Echeverría was elected president in 1970. His government had to contend with mistrust of Mexicans and increasing economic problems. He instituted electoral reforms.[88][89]

In the 1980s the first cracks emerged in the PRI's complete political dominance. In Baja California, the PAN candidate was elected as governor. When De la Madrid chose Carlos Salinas de Gortari as the candidate for the PRI, and therefore a foregone presidential victor, Cuauhtémoc Cárdenas, son of former President Lázaro Cárdenas, broke with the PRI and challenged Salinas in the 1988 elections. In 1988 there was massive electoral fraud, with results showing that Salinas had won the election by the narrowest percentage ever. There were massive protests in Mexico City over the stolen election. Salinas took the oath of office on 1 December 1988.[90] In 1990 the PRI was famously described by Mario Vargas Llosa as the "perfect dictatorship", but by then there had been major challenges to the PRI's hegemony.[91][92][93]
Salinas embarked on a program of neoliberal reforms that fixed the exchange rate of the peso, controlled inflation, opened Mexico to foreign investment, and began talks with the U.S. and Canada to join their free-trade agreement. To do that, the Constitution of 1917 was amended in several important ways. Article 27, which had allowed the government to expropriate natural resources and distribute land, was amended to end agrarian reform and to guarantee private owners' property rights. The anti-clerical articles that muzzled religious institutions, especially the Catholic Church, were amended and Mexico reestablished diplomatic relations with the Holy See. Signing on to the North American Free Trade Agreement (NAFTA) removed Mexico's autonomy over trade policy. The agreement came into effect on 1 January 1994; the same day, the Zapatista Army of National Liberation (EZLN) in Chiapas began armed peasant rebellion against the federal government, which captured a few towns but brought world attention to the situation in Mexico. The armed conflict was short-lived and has continued as a non-violent opposition movement against neoliberalism and globalization. In 1994, following the assassination of the PRI's presidential candidate Luis Donaldo Colosio, Salinas was succeeded by victorious PRI candidate Ernesto Zedillo. Salinas left Zedillo's government to deal with the Mexican peso crisis, requiring a $50 billion IMF bailout. Major macroeconomic reforms were started by Zedillo, and the economy rapidly recovered and growth peaked at almost 7% by the end of 1999.[94]
Contemporary Mexico

In 2000, after 71 years, the PRI lost a presidential election to Vicente Fox of the opposition conservative National Action Party (PAN). In the 2006 presidential election, Felipe Calderón from the PAN was declared the winner, with a very narrow margin (0.58%) over leftist politician Andrés Manuel López Obrador of the Party of the Democratic Revolution (PRD).[95] López Obrador, however, contested the election and pledged to create an "alternative government".[96]
After twelve years, in 2012, the PRI won the presidency again with the election of Enrique Peña Nieto. However, he won with a plurality of about 38% and did not have a legislative majority.[97]
After founding the new political party MORENA, Andrés Manuel López Obrador won the 2018 presidential election with over 50% of the vote. His political coalition, led by his left-wing party founded after the 2012 elections, included parties and politicians from all over the political spectrum. The coalition also won a majority in both the upper and lower Congress chambers. His success is attributed to the country's other strong political alternatives exhausting their chances as well as the politician adopting a moderate discourse with a focus on conciliation.[98]
Mexico has contended with high crime rates, official corruption, narcotrafficking, and a stagnant economy. Many state-owned industrial enterprises were privatized starting in the 1990s, with neoliberal reforms, but Pemex, the state-owned petroleum company is only slowly being privatized, with exploration licenses being issued.[99] In a push against government corruption, the ex-CEO of Pemex has been arrested.[100]
Although there were fears of electoral fraud in Mexico's 2018 presidential elections,[101] the results gave a mandate to AMLO.[102] Andrés Manuel López Obrador won a landslide victory in the July 2018 presidential elections and became the first leftwing president for decades.[103] Claudia Sheinbaum a Mexican politician, scientist, was elected president-elect of Mexico, the first woman to be elected to the position in 2024.[104]
Geography


Mexico is located between latitudes 14° and 33°N, and longitudes 86° and 119°W in the southern portion of North America. Almost all of Mexico lies in the North American Plate, with small parts of the Baja California peninsula on the Pacific and Cocos Plates. Geophysically, some geographers include the territory east of the Isthmus of Tehuantepec (around 12% of the total) within Central America.[105] Geopolitically, however, Mexico is entirely considered part of North America, along with Canada and the United States.[106]
Mexico's total area is 1,972,550 km2 (761,606 sq mi), making it the world's 13th largest country by total area. It has coastlines on the Pacific Ocean and Gulf of California, as well as the Gulf of Mexico and Caribbean Sea, the latter two forming part of the Atlantic Ocean.[107] Within these seas are about 6,000 km2 (2,317 sq mi) of islands (including the remote Pacific Guadalupe Island and the Revillagigedo Islands). From its farthest land points, Mexico is a little over 2,000 mi (3,219 km) in length. Mexico has nine distinct regions: Baja California, the Pacific Coastal Lowlands, the Mexican Plateau, the Sierra Madre Oriental, the Sierra Madre Occidental, the Cordillera Neo-Volcánica, the Gulf Coastal Plain, the Southern Highlands, and the Yucatán Peninsula.[108] Although Mexico is large, much of its land mass is incompatible with agriculture due to aridity, soil, or terrain. In 2018, an estimated 54.9% of land is agricultural; 11.8% is arable; 1.4% is in permanent crops; 41.7% is permanent pasture; and 33.3% is forest.[109]
Mexico is crossed from north to south by two mountain ranges known as Sierra Madre Oriental and Sierra Madre Occidental, which are the extension of the Rocky Mountains from northern North America. From east to west at the center, the country is crossed by the Trans-Mexican Volcanic Belt also known as the Sierra Nevada. A fourth mountain range, the Sierra Madre del Sur, runs from Michoacán to Oaxaca. The majority of the Mexican central and northern territories are located at high altitudes, and as such the highest elevations are found at the Trans-Mexican Volcanic Belt: Pico de Orizaba (5,700 m or 18,701 ft), Popocatépetl (5,462 m or 17,920 ft) and Iztaccihuatl (5,286 m or 17,343 ft) and the Nevado de Toluca (4,577 m or 15,016 ft). An important geologic feature of the Yucatán peninsula is the Chicxulub crater. The scientific consensus is that the Chicxulub impactor was responsible for the Cretaceous–Paleogene extinction event. Mexico is subject to several natural hazards, including hurricanes on both coasts, tsunamis on the Pacific coast, and volcanism.[110]
Climate

The climate of Mexico is quite varied due to the country's size and topography. Tropic of Cancer effectively divides the country into temperate and tropical zones. Land north of the Tropic of Cancer experiences cooler temperatures during the winter months. South of the Tropic of Cancer, temperatures are fairly constant year-round and vary solely as a function of elevation. This gives Mexico one of the world's most diverse weather systems. Maritime air masses bring seasonal precipitation from May until August. Many parts of Mexico, particularly the north, have a dry climate with only sporadic rainfall, while parts of the tropical lowlands in the south average more than 2,000 mm (78.7 in) of annual precipitation. For example, many cities in the north like Monterrey, Hermosillo, and Mexicali experience temperatures of 40 °C (104 °F) or more in summer. In the Sonoran Desert temperatures reach 50 °C (122 °F) or more.[111]
Descriptors of regions are by temperature,[citation needed] with the tierra caliente (hot land) being coastal up to 900 meters; tierra templada (temperate land) being from 1,800 meters; tierra fría (cold land) extending to 3,500 meters. Beyond the cold lands are the páramos, alpine pastures, and the tierra helada (frozen land) (4,000-4,200 meters) in central Mexico. Areas south of the Tropic of Cancer with elevations up to 1,000 m (3,281 ft) (the southern parts of both coastal plains as well as the Yucatán Peninsula), have a yearly median temperature between 24 and 28 °C (75.2 and 82.4 °F). Temperatures here remain high throughout the year, with only a 5 °C (9 °F) difference between winter and summer median temperatures. Both Mexican coasts, except for the south coast of the Bay of Campeche and northern Baja California, are also vulnerable to serious hurricanes during the summer and fall. Although low-lying areas north of the Tropic of Cancer are hot and humid during the summer, they generally have lower yearly temperature averages (from 20 to 24 °C or 68.0 to 75.2 °F) because of more moderate conditions during the winter.[111]
Biodiversity

Mexico ranks fourth[112] in the world in biodiversity and is one of the 17 megadiverse countries. With over 200,000 different species, Mexico is home of 10–12% of the world's biodiversity.[113] Mexico ranks first in biodiversity in reptiles with 707 known species, second in mammals with 438 species, fourth in amphibians with 290 species, and fourth in flora, with 26,000 different species.[114] Mexico is also considered the second country in the world in ecosystems and fourth in overall species.[115] About 2,500 species are protected by Mexican legislation.[115] In 2002[update], Mexico had the second fastest rate of deforestation in the world, second only to Brazil.[116] It had a 2019 Forest Landscape Integrity Index mean score of 6.82/10, ranking it 63rd globally out of 172 countries.[117] According to SGI there is Deforestation and soil erosion especially in rural areas of Mexico. In the 2022 report it was noted environmental protection laws have improved in major cities but remain unenforced or unregulated in rural regions.[118]

In Mexico, 170,000 square kilometers (65,637 sq mi) are considered "Protected Natural Areas". These include 34 biosphere reserves (unaltered ecosystems), 67 national parks, 4 natural monuments (protected in perpetuity for their aesthetic, scientific or historical value), 26 areas of protected flora and fauna, 4 areas for natural resource protection (conservation of soil, hydrological basins, and forests) and 17 sanctuaries (zones rich in diverse species).[113] Plants indigenous to Mexico are grown in many parts of the world and integrated into their national cuisines. Some of Mexico's native culinary ingredients include maize, tomato, beans, squash, chocolate, vanilla, avocado, guava, chayote, epazote, camote, jícama, nopal, zucchini, tejocote, huitlacoche, sapote, mamey sapote, and a great variety of chiles, such as the habanero and the jalapeño. Most of these names come from the indigenous language of Nahuatl. Tequila, the distilled alcoholic drink made from cultivated agave cacti is a major industry. Because of its high biodiversity Mexico has also been a frequent site of bioprospecting by international research bodies.[119] The first highly successful instance was the discovery in 1947 of the tuber "Barbasco" (Dioscorea composita) which has a high content of diosgenin, revolutionizing the production of synthetic hormones in the 1950s and 1960s and eventually leading to the invention of combined oral contraceptive pills.[120]
Government and politics


The United Mexican States are a federation whose government is representative, democratic, and republican based on a presidential system according to the 1917 Constitution. The Constitution establishes three levels of government: the federal Union, the state governments, and the municipal governments.
The federal legislature is the bicameral Congress of the Union, composed of the Senate of the Republic and the Chamber of Deputies. The Congress makes federal law, declares war, imposes taxes, approves the national budget and international treaties, and ratifies diplomatic appointments.[121] The federal Congress, as well as the state legislatures, are elected by a system of parallel voting that includes plurality and proportional representation.[122] The Chamber of Deputies has 500 deputies. Of these, 300 are elected by plurality vote in single-member districts (the federal electoral districts) and 200 are elected by proportional representation with closed party lists[123] for which the country is divided into five electoral constituencies.[124] The Senate comprises 128 senators: 64 (two for each state and two for Mexico City) are elected by plurality vote in pairs, 32 are the first minority or first-runner-up (one for each state and one for Mexico City), and 32 are elected by proportional representation from national closed party lists.[123]
The executive is the President of the United Mexican States, who is the head of state and government, as well as the commander-in-chief of the Mexican military forces. The President also appoints the Cabinet and other officers. The President is responsible for executing and enforcing the law and has the power to veto bills.[125]
The highest organ of the judicial branch of government is the Supreme Court of Justice, the national supreme court, which has eleven judges appointed by the President and approved by the Senate. The Supreme Court of Justice interprets laws and judges cases of federal competency. Other institutions of the judiciary are the Federal Electoral Tribunal, collegiate, unitary, and district tribunals, and the Council of the Federal Judiciary.[126]
Three parties have historically been the dominant parties in Mexican politics: the Institutional Revolutionary Party (PRI), a catch-all party[127] and member of the Socialist International[128] that was founded in 1929 to unite all the factions of the Mexican Revolution and held an almost hegemonic power in Mexican politics since then; the National Action Party (PAN), a conservative party founded in 1939 and belonging to the Christian Democrat Organization of America;[129] and the Party of the Democratic Revolution (PRD) a left-wing party,[130] founded in 1989 as the successor of the coalition of socialists and liberal parties.
Foreign relations

The foreign relations of Mexico are directed by the President of Mexico[131] and managed through the Ministry of Foreign Affairs.[132] The principles of the foreign policy are constitutionally recognized in the Article 89, Section 10, which include: respect for international law and legal equality of states, their sovereignty and independence, trend to non-interventionism in the domestic affairs of other countries, peaceful resolution of conflicts, and promotion of collective security through active participation in international organizations.[131] Since the 1930s, the Estrada Doctrine has served as a crucial complement to these principles.[133]
Mexico is a founding member of several international organizations, most notably the United Nations,[134] the Organization of American States,[135] the Organization of Ibero-American States,[136] the OPANAL[137] and the CELAC.[138] In 2008, Mexico contributed over 40 million dollars to the United Nations regular budget.[139] In addition, it was the only Latin American member of the Organisation for Economic Co-operation and Development since it joined in 1994 until Chile gained full membership in 2010.[140][141]
Mexico is considered a regional power[142][143] hence its presence in major economic groups such as the G8+5 and the G-20. Since the 1990s Mexico has sought a reform of the United Nations Security Council and its working methods[144] with the support of Canada, Italy, Pakistan and other nine countries, which form a group informally called the Coffee Club.[145]
Military


The Mexican Armed Forces are administered by the Secretariat of National Defense (Secretaria de Defensa Nacional, SEDENA). There are two branches: the Mexican Army (which includes the Mexican Air Force), and the Mexican Navy. The Secretariat of Public Security and Civil Protection has jurisdiction over the National Guard, which was formed in 2019 from the disbanded Federal Police and military police of the Army and Navy. Figures vary on personnel, but as of are approximately 223,000 armed forces personnel (160,000 Army; 8,000 Air Force; 55,000 Navy, including about 20,000 Marines); approximately 100,000 National Guard (2021). Government expenditures on the military are a small proportion of GDP: 0.7% of GDP (2021 est.), 0.6% of GDP (2020).[146]
The Mexican Armed Forces maintain significant infrastructure, including facilities for the design, research, and testing of weapons, vehicles, aircraft, naval vessels, defense systems and electronics; military industry manufacturing centers for building such systems, and advanced naval dockyards that build heavy military vessels and advanced missile technologies. Since the 1990s, when the military escalated its role in the war on drugs, increasing importance has been placed on acquiring airborne surveillance platforms, aircraft, helicopters, digital war-fighting technologies,[147] urban warfare equipment and rapid troop transport.[148] Mexico has the capabilities to manufacture nuclear weapons, but abandoned this possibility with the Treaty of Tlatelolco in 1968 and pledged to use its nuclear technology only for peaceful purposes.[149] Mexico signed the UN treaty on the Prohibition of Nuclear Weapons.[150]
Historically, Mexico has remained neutral in international conflicts,[151] with the exception of World War II. However, in recent years some political parties have proposed an amendment of the Constitution to allow the Mexican Army, Air Force or Navy to collaborate with the United Nations in peacekeeping missions, or to provide military help to countries that officially ask for it.[152]
Law enforcement and human rights


The Mexican Federal Police was dissolved in 2019 by a constitutional amendment during the administration of President López Obrador and the Mexican National Guard established, amalgamating units of the Federal Police, Military Police, and Naval Police.[153] As of 2022, the National Guard is an estimated at 110,000. López Obrador has increasingly used military forces for domestic law enforcement, particularly against drug cartels.[154] There have been serious abuses of power reported in security operations in the southern part of the country and in indigenous communities and poor urban neighborhoods. The National Human Rights Commission has had little impact in reversing this trend, engaging mostly in documentation but failing to use its powers to issue public condemnations to the officials who ignore its recommendations.[155] Most Mexicans have low confidence in the police or the judicial system, and therefore, few crimes are actually reported by the citizens.[156] There have been public demonstrations of outrage against what is considered a culture of impunity.[157]
Mexico has fully recognised same-sex marriage since 2022,[158] and anti-discrimination laws regarding sexual orientation have existed in the nation since 2003.[159] However, hate crimes towards the LGBT community remain an issue in Mexico.[160][161] Other crime and human rights violations in Mexico have been criticized, including enforced disappearances (kidnappings), abuses against migrants, extrajudicial killings, gender-based violence, especially femicide, and attacks on journalists and human rights advocates.[162] A 2020 report by the BBC gives statistics on crime in Mexico, with 10.7 million households with at least one victim of crime.[163] As of May 2022, 100,000 people are officially listed as missing, most since 2007 when President Calderón attempted to stop the drug cartels.[164] Drug cartels remain a major issue in Mexico, with a proliferation of smaller cartels when larger ones are broken up and increasingly the use of more sophisticated military equipment and tactics.[165][166]
Mexico's drug war, ongoing since 2006, has left over 120,000 dead and perhaps another 37,000 missing.[30] Mexico's National Geography and Statistics Institute estimated that in 2014, one-fifth of Mexicans were victims of some sort of crime.[167] The mass kidnapping of 43 students in Iguala on 26 September 2014 triggered nationwide protests against the government's weak response to the disappearances and widespread corruption that gives free rein to criminal organizations.[168] More than 100 journalists and media workers have been killed or disappeared since 2000, and most of these crimes remained unsolved, improperly investigated, and with few perpetrators arrested and convicted.[169][170]
Administrative divisions
The boundaries and constituent units of Mexico evolved from its colonial-era origins. Central America peacefully separated from Mexico after independence in 1821. Yucatán was briefly an independent republic. Texas separated in the Texas Revolution and when it was annexed to the U.S. in 1845, it set the stage for the Mexican–American War and major territorial loss to the U.S. The sale of northern territory known in the U.S. as the Gadsden Purchase was the last loss of Mexican territory. The United Mexican States are a federation of 31 free and sovereign states, which form a union that exercises a degree of jurisdiction over Mexico City.[171] Each state has its constitution, congress, and a judiciary, and its citizens elect by direct voting a governor for a six-year term, and representatives to their respective unicameral state congresses for three-year terms.[172]
Mexico City is a special political division that belongs to the federation as a whole and not to a particular state.[171] Formerly known as the Federal District, its autonomy was previously limited relative to that of the states.[173] It dropped this designation in 2016 and is in the process of achieving greater political autonomy by becoming a federal entity with its constitution and congress.[174] The states are divided into municipalities, the smallest administrative political entity in the country, governed by a mayor or municipal president (presidente municipal), elected by its residents by plurality.[175]
Economy



As of April 2018, Mexico has the 15th largest nominal GDP (US$1.15 trillion) and the 11th largest by purchasing power parity (US$2.45 trillion). GDP annual average growth was 2.9% in 2016 and 2% in 2017.[176] Agriculture has comprised 4% of the economy over the last two decades, while industry contributes 33% (mostly automotive, oil, and electronics) and services (notably financial services and tourism) contribute 63%.[176] Mexico's GDP in PPP per capita was US$18,714.05. The World Bank reported in 2009 that the country's gross national income in market exchange rates was the second highest in Latin America, after Brazil at US$1,830.392 billion,[177] which led to the highest income per capita in the region at $15,311.[178][179]
Mexico is established as an upper-middle-income country. After the slowdown of 2001 the country recovered and grew 4.2, 3.0 and 4.8 percent in 2004, 2005 and 2006,[180] even though it is considered to be well below Mexico's potential growth.[181] The International Monetary Fund predicts growth rates of 2.3% and 2.7% for 2018 and 2019, respectively.[176] By 2050, Mexico could potentially become the world's fifth or seventh-largest economy.[182][183]
The electronics industry of Mexico has grown enormously within the last decade. Mexico has the sixth largest electronics industry in the world after China, the United States, Japan, South Korea, and Taiwan. Mexico is the second-largest exporter of electronics to the United States where it exported $71.4 billion worth of electronics in 2011.[184] The Mexican electronics industry grew 20% between 2010 and 2011, up from its constant growth rate of 17% between 2003 and 2009.[184] Currently electronics represent 30% of Mexico's exports.[184]
Mexico produces the most automobiles of any North American nation.[185] The industry produces technologically complex components and engages in some research and development activities.[186] The "Big Three" (General Motors, Ford and Chrysler) have been operating in Mexico since the 1930s, while Volkswagen and Nissan built their plants in the 1960s.[187] In Puebla alone, 70 industrial part-makers cluster around Volkswagen.[186] In the 2010s expansion of the sector was surging. In September 2016 Kia opened a $1 billion factory in Nuevo León,[188] with Audi also opening an assembling plant in Puebla the same year.[189] BMW, Mercedes-Benz and Nissan currently have plants in construction.[190] The domestic car industry is represented by DINA S.A., which has built buses and trucks since 1962,[191] and the new Mastretta company that builds the high-performance Mastretta MXT sports car.[192] In 2006, trade with the United States and Canada accounted for almost 50% of Mexico's exports and 45% of its imports.[11]
During the first three quarters of 2010, the United States had a $46.0 billion trade deficit with Mexico.[193] In August 2010 Mexico surpassed France to become the 9th largest holder of US debt.[194] The commercial and financial dependence on the US is a cause for concern.[195] The remittances from Mexican citizens working in the United States are significant; after dipping during the 2008 Great Recession and again during COVID-19 pandemic in 2021 they are topping other sources of foreign income.[196][197] Remittances are directed to Mexico by direct links from a U.S. government banking program.[198]
Although multiple international organizations coincide and classify Mexico as an upper middle income country, or a middle class country,[199][200] Mexico's National Council for the Evaluation of Social Development Policy (CONEVAL), which is the organization in charge to measure the country's poverty reports that a huge percentage of Mexico's population lives in poverty. According to said council, from 2006 to 2010 (the year on which the CONEVAL published its first nationwide report of poverty) the portion of Mexicans who live in poverty rose from 18%–19%[201] to 46% (52 million people).[202] Despite this situation, CONEVAL reported in 2023 that the country's poverty rate has been decreasing in recent years, as the organization registered, within the period between 2018 and 2022, a 5.6% decrease, from 41.9% to 36.3% (from 51.9 million to 46.8 million people), according to its Multidimensional Poverty Index, though the extreme poverty rate rose by 0.1% (410 thousand people) within the same period, remaining at 7.1% (9.1 million people), and the number of people lacking access to healthcare services has significantly increased, from 16.2% to 39.1% (50.4 million people),[203][204] though some specialists have expressed a degree of doubt regarding the accuracy of these rates.[205] According to the OECD's own poverty line (defined as the percentage of a country's population who earns 60%[206] or less of the national median income) 20% of Mexico's population lived in a situation of poverty in 2019.[207]
Among the OECD countries, Mexico has the second-highest degree of economic disparity between the extremely poor and extremely rich, after Chile – although it has been falling over the last decade, being one of few countries in which this is the case.[208] The bottom ten percent in the income hierarchy disposes of 1.36% of the country's resources, whereas the upper ten percent dispose of almost 36%. The OECD also notes that Mexico's budgeted expenses for poverty alleviation and social development are only about a third of the OECD average.[209] This is also reflected by the fact that infant mortality in Mexico is three times higher than the average among OECD nations whereas its literacy levels are in the median range of OECD nations. Nevertheless, according to a Goldman Sachs report published in 2007, by 2050 Mexico will have the 5th largest economy in the world.[210] According to a 2008 UN report the average income in a typical urbanized area of Mexico was $26,654, while the average income in rural areas just miles away was only $8,403.[211] Daily minimum wages are set annually. The daily minimum wage will be $248.93 Mexican pesos (US$13.24) in 2024 ($375 in the country's northern border), making it comparable to the minimum wages of countries like Uruguay, Chile and Ecuador. The minimum wage has rapidly increased throughout the last few years, as it was set at 88.15 pesos in 2018.[212]
Communications

The telecommunications industry is mostly dominated by Telmex (Teléfonos de México), previously a government monopoly privatized in 1990. By 2006, Telmex had expanded its operations to Colombia, Peru, Chile, Argentina, Brazil, Uruguay, and the United States. Other players in the domestic industry are Axtel, Maxcom, Alestra, Marcatel, AT&T Mexico.[213] Because of Mexican orography, providing a landline telephone service at remote mountainous areas is expensive, and the penetration of line-phones per capita is low compared to other Latin American countries, at 40 percent; however, 82% of Mexicans over the age of 14 own a mobile phone. Mobile telephony has the advantage of reaching all areas at a lower cost, and the total number of mobile lines is almost two times that of landlines, with an estimation of 63 million lines.[214] The telecommunication industry is regulated by the government through Cofetel (Comisión Federal de Telecomunicaciones).
The Mexican satellite system is domestic and operates 120 earth stations. There is also extensive microwave radio relay network and considerable use of fiber-optic and coaxial cable.[214] Mexican satellites are operated by Satélites Mexicanos (Satmex), a private company, leader in Latin America and servicing both North and South America.[215] It offers broadcast, telephone, and telecommunication services to 37 countries in the Americas, from Canada to Argentina. Through business partnerships Satmex provides high-speed connectivity to ISPs and Digital Broadcast Services.[216] Satmex maintains its satellite fleet with most of the fleet being designed and built in Mexico. Major players in the broadcasting industry are Televisa, the largest Mexican media company in the Spanish-speaking world,[217] TV Azteca and Imagen Televisión.
Energy

Energy production in Mexico is managed by the state-owned companies Federal Commission of Electricity and Pemex. Pemex, the public company in charge of exploration, extraction, transportation, and marketing of crude oil and natural gas, as well as the refining and distribution of petroleum products and petrochemicals, is one of the largest companies in the world by revenue, making US$86 billion in sales a year.[218][219][220] Mexico is the sixth-largest oil producer in the world, with 3.7 million barrels per day.[221] In 1980 oil exports accounted for 61.6% of total exports; by 2000 it was only 7.3%.[186] The largest hydro plant in Mexico is the 2,400 MW Manuel Moreno Torres Dam in Chicoasén, Chiapas, in the Grijalva River. This is the world's fourth most productive hydroelectric plant.[222]
Mexico is the country with the world's third-largest solar potential.[223] The country's gross solar potential is estimated at 5kWh/m2 daily, which corresponds to 50 times the national electricity generation.[224] Currently, there is over 1 million square meters of solar thermal panels[225] installed in Mexico, while in 2005, there were 115,000 square meters of solar PV (photo-voltaic). It is expected that in 2012 there will be 1,8 million square meters of installed solar thermal panels.[225] The project named SEGH-CFE 1, located in Puerto Libertad, Sonora, Northwest of Mexico, will have a capacity of 46.8 MW from an array of 187,200 solar panels when complete in 2013.[226] All of the electricity will be sold directly to the CFE and absorbed into the utility's transmission system for distribution throughout their existing network. At an installed capacity of 46.8 MWp, when complete in 2013, the project will be the first utility-scale project of its kind in Mexico and the largest solar project of any kind in Latin America.
Science and technology

The National Autonomous University of Mexico was officially established in 1910,[227] and the university became one of the most important institutes of higher learning in Mexico.[228] UNAM provides world class education in science, medicine, and engineering.[229] Many scientific institutes and new institutes of higher learning, such as National Polytechnic Institute (founded in 1936),[230] were established during the first half of the 20th century. Most of the new research institutes were created within UNAM. Twelve institutes were integrated into UNAM from 1929 to 1973.[231] In 1959, the Mexican Academy of Sciences was created to coordinate scientific efforts between academics.
In 1995, the Mexican chemist Mario J. Molina shared the Nobel Prize in Chemistry with Paul J. Crutzen and F. Sherwood Rowland for their work in atmospheric chemistry, particularly concerning the formation and decomposition of ozone.[232] Molina, an alumnus of UNAM, became the first Mexican citizen to win the Nobel Prize in science.[233]
In recent years, the largest scientific project being developed in Mexico was the construction of the Large Millimeter Telescope (Gran Telescopio Milimétrico, GMT), the world's largest and most sensitive single-aperture telescope in its frequency range.[234] It was designed to observe regions of space obscured by stellar dust. Mexico was ranked 58th in the Global Innovation Index in 2023.[235][236]
Tourism

As of 2017, Mexico was the 6th most visited country in the world and had the 15th highest income from tourism in the world which is also the highest in Latin America.[237] The vast majority of tourists come to Mexico from the United States and Canada followed by Europe and Asia. A smaller number also come from other Latin American countries.[238] In the 2017 Travel and Tourism Competitiveness Report, Mexico was ranked 22nd in the world, which was 3rd in the Americas.[239]
The coastlines of Mexico are rich in sunny beach stretches. According to the Constitution of Mexico Article 27, the entirety of the coastlines is under federal ownership. On the Yucatán peninsula, one of the most popular beach destinations is the resort town of Cancún, especially among university students during spring break. To the south of Cancun is the coastal strip called Riviera Maya which includes the beach town of Playa del Carmen and the ecological parks of Xcaret and Xel-Há. To the south of Cancún is the town of Tulum, notable for its ruins of Maya civilization. Other notable tourist destinations include Acapulco with crowded beaches and multi-story hotels on the shores. At the southern tip of the Baja California peninsula is the resort town of Cabo San Lucas, noted for its marlin fishing.[240] Closer to the United States border is the weekend draw of San Felipe, Baja California.[citation needed]
In Mexican cities along the Mexico–United States border, the most lucrative hospitality industry is now medical tourism, with remnants of the traditional motivations that drove tourists to Mexico's northern borderlands for nearly a century. Dominant medical tourism for tourism planning are the purchase of medication, dentistry, elective surgery, optometry, and chiropractic.[241]
Transportation

Despite its difficult topography, Mexico's roadway is extensive and most areas in the country are covered. The roadway network in Mexico has an extent of 366,095 km (227,481 mi),[242] of which 116,802 km (72,577 mi) are paved,[243] making it 9th largest of any country[244] and has the 7th best connectivity index in the world.[245] Of these, 10,474 km (6,508 mi) are multi-lane expressways: 9,544 km (5,930 mi) are four-lane highways and the rest have 6 or more lanes.[243]
Starting in the late nineteenth century, Mexico was one of the first Latin American countries to promote railway development,[156] and the network covers 30,952 km (19,233 mi). The Secretary of Communications and Transport of Mexico proposed a high-speed rail link that will transport its passengers from Mexico City to Guadalajara, Jalisco.[246][247] The train, which will travel at 300 kilometers per hour (190 miles per hour),[248] will allow passengers to travel from Mexico City to Guadalajara in just 2 hours.[248] The whole project was projected to cost 240 billion pesos, or about 25 billion US$[246] and is being paid for jointly by the Mexican government and the local private sector including one of the wealthiest men in the world, Mexico's billionaire business tycoon Carlos Slim.[249] The government of the state of Yucatán is also funding the construction of a high speed line connecting the cities of Cozumel to Mérida and Chichen Itza and Cancún.[250]
Mexico has 233 airports with paved runways; of these, 35 carry 97% of the passenger traffic.[citation needed] The Mexico City International Airport remains the busiest in Latin America and the 36th busiest in the world[251] transporting 45 million passengers a year.[252]
Demographics

According to Mexico's National Geography and Statistics Institute, the country's estimated population in 2022 is 129,150,971.[253] In 2017, Mexico had 123.5 million inhabitants.[254] Since at least the 1970s, Mexico has been the most populous Spanish-speaking country in the world.[255]
Throughout the 19th century, the population of Mexico had barely doubled. This trend continued during the first two decades of the 20th century. In 1900, the Mexican population was 13.6 million.[256] The 1921 census reported a loss of about 1 million inhabitants. The Mexican Revolution (c. 1910–1920) greatly impacted population increases. The growth rate increased dramatically between the 1930s and the 1980s when the country registered growth rates of over 3% (1950–1980). The Mexican population doubled in twenty years, and at that rate, it was expected that by 2000 there would be 120 million people living in Mexico. Mexico's population grew from 70 million in 1982 to 120 million in 2015.[257]
Life expectancy increased from 36 years (in 1895) to 72 years (in 2000)
Ethnicity and race
Mexico's population is highly diverse, but research on Mexican ethnicity has felt the impact of nationalist discourses on identity.[258][259][260] Since the 1930s, the Mexican government has promoted the view that all Mexicans are part of the Mestizo community, within which they are distinguished only by residence in or outside of an indigenous community, degree of fluency in an indigenous language, and degree of adherence to indigenous customs.[261][262]
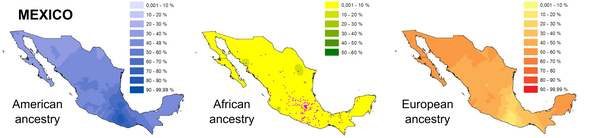
It is not until very recently that the Mexican government began conducting surveys that consider other ethnic groups that live in the country, such as Afro-Mexicans (who comprised 2% of Mexico's population in 2020)[12] or White Mexicans (47%).[263][264] Less numerous groups in Mexico such as Asians and Middle Easterners are also accounted for, with numbers of around 1% each. While Mestizos are a prominent ethnic group in contemporary Mexico, the subjective and ever-changing definition of this category has led to its estimations being imprecise, having been observed that many Mexicans do not identify as Mestizos,[265][266] favoring instead ethnoracial labels such as White or Indigenous due to having more consistent and "static" definitions.[267]
Languages
Spanish is the de facto national language spoken by the vast majority of the population, making Mexico the world's most populous Hispanophone country.[269][255] Mexican Spanish refers to the varieties of the language spoken in the country, which differs from one region to another in sound, structure, and vocabulary.[270]

The federal government officially recognizes sixty-eight linguistic groups and 364 varieties of indigenous languages.[271] It is estimated that around 8.3 million citizens speak these languages,[272] with Nahuatl being the most widely spoken by more than 1.7 million, followed by Yucatec Maya used daily by nearly 850,000 people. Tzeltal and Tzotzil, two other Mayan languages, are spoken by around half a million people each, primarily in the southern state of Chiapas.[272] Mixtec and Zapotec, with an estimated 500,000 native speakers each, are two other prominent language groups.[272] Since its creation in March 2003, the National Indigenous Languages Institute has been in charge of promoting and protecting the use of the country's indigenous languages, through the General Law of Indigenous Peoples' Linguistic Rights, which recognizes them de jure as "national languages" with status equal to that of Spanish.[273] That notwithstanding, in practice, indigenous peoples often face discrimination and do not have full access to public services such as education and healthcare, or to the justice system, as Spanish is the prevailing language.[274]
Aside from indigenous languages, there are several minority languages spoken in Mexico due to international migration such as Low German by the 80,000-strong Mennonite population, primarily settled in the northern states, fueled by the tolerance of the federal government towards this community by allowing them to set their educational system compatible with their customs and traditions.[275] The Chipilo dialect, a variance of the Venetian language, is spoken in the town of Chipilo, located in the central state of Puebla, by around 2,500 people, mainly descendants of Venetians that migrated to the area in the late 19th century.[276] Furthermore, English is the most commonly taught foreign language in Mexico. It is estimated that nearly 24 million, or around a fifth of the population, study the language through public schools, private institutions, or self-access channels.[277] However, a high level of English proficiency is limited to only 5% of the population.[278] Moreover, French is the second most widely taught foreign language, as every year between 200,000 and 250,000 Mexican students enroll in language courses.[279][280][281]
Emigration and immigration

In the early 1960s, around 600,000 Mexicans lived abroad, which increased sevenfold by the 1990s to 4.4 million.[282] At the turn of the 21st century, this figure more than doubled to 9.5 million.[282] Between 1965 and 2015, more than 16 million Mexicans migrated to the United States alone—by far the top destination for both temporary and permanent migration—representing one of the largest mass migrations in modern history.[283]
As of 2019, it is estimated that 11.7 million Mexicans live outside Mexico, in addition to 13.5 million born abroad and another 12 million descendants; the vast majority of this combined population (98–99%) are in the U.S.[284] The number of overseas Mexicans peaked at roughly 12.9 million sometime between 2007[283] and 2018,[282] owing to a variety of factors, including increased return migration from the U.S. coupled with reduced migration abroad.[283]
The majority of Mexicans abroad have settled in U.S. states at or near the Mexican border, such as California and Texas, and in urban areas of Illinois, North Carolina, and Georgia; the largest Mexican communities outside Mexico are in the metropolitan areas of Los Angeles, Chicago, Houston and Dallas–Fort Worth.[285] As a result of these major migration flows in recent decades, an estimated 37.2 million U.S. residents, or 11.2% of the country's population, identified as being of full or partial Mexican ancestry.[286][287]
Among the remaining 2% of Mexican expatriates not residing in the U.S., the most popular destinations are Canada (86,780), primarily the provinces of Ontario and Quebec,[288] followed by Spain (60,850) and Germany (20,270);[289] the latter two countries account for two-thirds of all Mexicans living in Europe.[282] It is estimated that 69,000 Mexicans live in Latin America, led by Guatemala (18,870) followed by Bolivia (10,610), Chile (10,560), and Panama (5,000).[282]
As of 2020, an estimated 1.2 million foreigners settled in Mexico,[290] up from nearly 1 million in 2010.[291] In 2021, Mexico officially received 68,000 new immigrants, a 16% increase from the prior year;[292] the overall number of migrants, including those unauthorized to enter or stay in the country, may be higher than official figures.[293] The vast majority of migrants in Mexico come from the United States (900,000), making Mexico the top destination for U.S. citizens abroad.[294] The second largest group comes from neighboring Guatemala (54,500), followed by Spain (27,600).[290] Other major sources of migration are fellow Latin American countries, which include Colombia (20,600), Argentina (19,200) and Cuba (18,100).[290]
Historically, and relative to other countries in the Western Hemisphere, Mexico has not been a destination of mass migration.[293] However, communities descended from the Lebanese diaspora and German-born Mennonites have had an outsized impact in the country's culture, particularly in its cuisine and traditional music.[295][296] At the turn of the 21st century, several trends have increased the number of foreigners residing in Mexico such as the 2008–2014 Spanish financial crisis,[297] increasing gang-related violence in the Northern Triangle of Central America,[298] the ongoing political and economic crisis in Venezuela,[299][300] and the automotive industry boom led by Japanese and South Korean investment.[301][302]
Urban areas
| Rank | Name | State | Pop. | Rank | Name | State | Pop. | ||
|---|---|---|---|---|---|---|---|---|---|
 Valley of Mexico  Monterrey |
1 | Valley of Mexico | Mexico City, State of Mexico, Hidalgo | 21,804,515 | 11 | Aguascalientes | Aguascalientes | 1,225,432 |  Guadalajara  Puebla–Tlaxcala |
| 2 | Monterrey | Nuevo León | 5,341,171 | 12 | San Luis Potosí | San Luis Potosí | 1,221,526 | ||
| 3 | Guadalajara | Jalisco | 5,286,642 | 13 | Mérida | Yucatán | 1,201,000 | ||
| 4 | Puebla–Tlaxcala | Puebla, Tlaxcala | 3,199,530 | 14 | Mexicali | Baja California | 1,031,779 | ||
| 5 | Toluca | State of Mexico | 2,353,924 | 15 | Saltillo | Coahuila | 1,031,779 | ||
| 6 | Tijuana | Baja California | 2,157,853 | 16 | Cuernavaca | Morelos | 1,028,589 | ||
| 7 | León | Guanajuato | 1,924,771 | 17 | Culiacán | Sinaloa | 1,003,530 | ||
| 8 | Querétaro | Querétaro | 1,594,212 | 18 | Morelia | Michoacán | 988,704 | ||
| 9 | Juárez | Chihuahua | 1,512,450 | 19 | Chihuahua | Chihuahua | 988,065 | ||
| 10 | La Laguna | Coahuila, Durango | 1,434,283 | 20 | Veracruz | Veracruz | 939,046 | ||
Religion
Religion in Mexico (2020 census)[304][305]
Although the Constitutions of 1857 and 1917 put limits on the role of the Roman Catholic Church in Mexico, Roman Catholicism remains the country's dominant religious affiliation. The 2020 census by the Instituto Nacional de Estadística y Geografía (National Institute of Statistics and Geography) gives Roman Catholicism as the main religion, with 77.7% (97,864,218) of the population, while 11.2% (14,095,307) belong to Protestant/Evangelical Christian denominations—including Other Christians (6,778,435), Evangelicals (2,387,133), Pentecostals (1,179,415), Jehovah's Witnesses (1,530,909), Seventh-day Adventists (791,109), and members of the Church of Jesus Christ of Latter-day Saints (337,998)—; 8.1% (9,488,671) declared having no religion; 0.4% (491,814) were unspecified.[12][306]
The 97,864,218[12] Catholics of Mexico constitute in absolute terms the second largest Catholic community in the world, after Brazil's.[307] 47% percent of them attend church services weekly.[308] The feast day of Our Lady of Guadalupe, the patron saint of Mexico, is celebrated on 12 December and is regarded by many Mexicans as the most important religious holiday of their country.[309] The denominations Pentecostal also have an important presence, especially in the cities of the border and in the indigenous communities. As of 2010, Pentecostal churches together have more than 1.3 million adherents, which in net numbers place them as the second Christian creed in Mexico. The situation changes when the different Pentecostal denominations are considered as separate entities. Migratory phenomena have led to the spread of different aspects of Christianity, including branches Protestants, Eastern Catholic Churches and Eastern Orthodox Church.[310]
The presence of Jews in Mexico dates back to 1521, when Hernán Cortés conquered the Aztecs, accompanied by several Conversos.[311] According to the 2020 census, there are 58,876 Jews in Mexico.[12] Islam in Mexico (with 7,982 members) is practiced mostly by Arab Mexicans.[12] In the 2010 census 36,764 Mexicans reported belonging to a spiritualist religion,[12] a category which includes a tiny Buddhist population.
According to Jacobo Grinberg, the survival of magic-religious rituals of the old indigenous groups is remarkable. There is often a syncretism between shamanism and Catholic traditions. Another religion of popular syncretism in Mexico (especially in recent years) is the Santería. This is mainly due to the large number of Cubans who settled in the territory after the Cuban Revolution. Even though Mexico was also a recipient of black slaves from Africa in the 16th century, the apogee of these cults is relatively new.[312] In general, popular religiosity is viewed with bad eyes by institutionally structured religions. One of the most exemplary cases of popular religiosity is the cult of Holy Dead (Santa Muerte). The Catholic hierarchy insists on describing it as a satanic cult. However, most of the people who profess this cult declare themselves to be Catholic believers. Other examples are the representations of the Passion of Christ and the celebration of Day of the Dead, which take place within the framework of the Catholic Christian imaginary, but under a very particular reinterpretation.[313]
Health

In the 1930s, Mexico made a commitment to rural health care, mandating that mostly urban medical students receive training in it and to make them agents of the state to assess marginal areas.[314] Since the early 1990s, Mexico entered a transitional stage in the health of its population and some indicators such as mortality patterns are identical to those found in highly developed countries like Germany or Japan.[315] Mexico's medical infrastructure is highly rated for the most part and is usually excellent in major cities,[316][317] but rural communities still lack equipment for advanced medical procedures, forcing patients in those locations to travel to the closest urban areas to get specialized medical care.[156] Social determinants of health can be used to evaluate the state of health in Mexico.
State-funded institutions such as Mexican Social Security Institute (IMSS) and the Institute for Social Security and Services for State Workers (ISSSTE) play a major role in health and social security. Private health services are also very important and account for 13% of all medical units in the country.[318] Medical training is done mostly at public universities with many specializations done in vocational or internship settings. Some public universities in Mexico, such as the University of Guadalajara, have signed agreements with the U.S. to receive and train American students in medicine. Health care costs in private institutions and prescription drugs in Mexico are on average lower than that of its North American economic partners.[316]
Education

As of 2020, the literacy rate in Mexico is 95.25%, a slight increase from 94.86% in 2018, and significantly higher than 82.99% in 1980.[319] Literacy between males and females is relatively equal.
According to most rankings, the publicly funded National Autonomous University of Mexico (UNAM) is the best university in the country. Other prominent public universities include the National Polythechnic Institute, the Metropolitan Autonomous University, the University of Guadalajara and the Autonomous University of Nuevo León and El Colegio de México.[320][321][322][323]
In terms of private academic institutions, among the most highly ranked is the Monterrey Institute of Technology and Higher Education; other prominent private universities include Universidad Iberoamericana, Universidad Panamericana, ITAM and Universidad Anáhuac.[320][321][322]
Culture

Mexican culture reflects a long and complex history of interactions between various peoples through migration, conquest, and trade. Three centuries of Spanish rule resulted in the blending of Spanish culture with those of different indigenous groups. Efforts to assimilate the native population into Christian European culture during the colonial era were only partially successful, with many pre-Columbian customs, traditions, and norms persisting regionally (particularly in rural areas) or becoming syncretized; conversely, many Spanish settlers integrated into local communities through acculturation or intermarriage. However, a high degree of stratification along the lines of class, ethnicity, and race perpetuated distinct subcultures.[324]
The Porfirian era (el Porfiriato) (1876–1911), which brough relative peace after four decades of civil unrest and war, saw the development of philosophy and art, often with government support. Since that time, as accentuated during the Mexican Revolution, cultural identity has had its foundation in mestizaje: the blending of different races and cultures, of which the indigenous (i.e. Amerindian) element is the core.[325] In light of the various ethnicities that formed the Mexican people, José Vasconcelos in La Raza Cósmica (The Cosmic Race) (1925) defined Mexico and Latin America to be the melting pot of all races (thus extending the definition of the mestizo) not only biologically but culturally as well.[326] Other Mexican intellectuals grappled with the idea of Lo Mexicano, which seeks "to discover the national ethos of Mexican culture."[327] Nobel laureate Octavio Paz explores the notion of a Mexican national character in The Labyrinth of Solitude.
Art

Painting is one of the oldest arts in Mexico. Cave painting in Mexican territory is about 7500 years old and has been found in the caves of the Baja California Peninsula. Pre-Columbian Mexico is present in buildings and caves, in Aztec codices, in ceramics, in garments, etc.; examples of this are the Maya mural paintings of Bonampak, or those of Teotihuacán, those of Cacaxtla and those of Monte Albán.[citation needed] Mural painting with Christian religious themes had an important flowering during the 16th century, early colonial era in newly constructed churches and monasteries. Examples can be found in Acolman, Actopan, Huejotzingo, Tecamachalco and Zinacantepec.[citation needed]
As with most art during the early modern era in the West, colonial-era Mexican art was religious during the sixteenth and seventeenth centuries. Starting in the late seventeenth century, and, most prominently in the eighteenth century, secular portraits and images of racial types, so-called casta painting appeared.[328] Important painters of the late colonial period were Juan Correa, Cristóbal de Villalpando and Miguel Cabrera. In early post-independence Mexico, nineteenth-century painting had a marked romantic influence; landscapes and portraits were the greatest expressions of this era. Hermenegildo Bustos is one of the most appreciated painters of the historiography of Mexican art. Other painters include Santiago Rebull, Félix Parra, Eugenio Landesio, and his noted pupil, the landscape artist José María Velasco.[329]

In the 20th century artists such as Diego Rivera, David Alfaro Siqueiros, and José Clemente Orozco, the so-called "Big Three" of Mexican muralism achieved worldwide recognition. They were commissioned by the Mexican government to paint large-scale historical murals on the walls of public buildings, which helped shape popular perceptions of the Mexican Revolution and Mexican cultural identity.[330] Frida Kahlo's largely personal portraiture is considered by many as the most important historical work by a female artist.[331]
In the 21st century, Mexico City became home to the highest concentration of art museums in the world. Institutions like the Museo Jumex, the largest collection of its kind, founded by collector Eugenio López Alonso and bolstered by art advisor Esthella Provas, changed the notion of contemporary art in Latin America.[332][333] The Museo Tamayo Arte Contemporaneous founded by Rufino Tamayo is also considered a preeminent institution and introduced foreign artists to a wider population.[334] The country is also an epicenter for International art galleries including Kurimanzutto and FF Projects,[335][336] and leading artists including Gabriel Orozco, Bosco Sodi, Stefan Brüggemann, and Mario García Torres.[337]
Architecture
The architecture of Mesoamerican civilizations evolved in style from simple to complex. Teotihuacan, designated a UNESCO World Heritage Site in 1987, is one of the foremost examples of ancient pyramid construction. The cities of the Maya stand out to modern architects as examples of integration between large urban centers (with elaborate stone construction) and a thick jungle, generally with a complex network of roads. Pre-Columbian Mesoamerica also saw distinctive architectural influences from the Puuc and oasiamerican peoples.

With the arrival of the Spanish, architectural theories of the Greco-Latin order with Arab influences were introduced. In the first few decades of Spanish presence in the continent, the high level of Christian missionary activity, especially by mendicant orders like the Dominicans or Franciscans, meant the construction of many monasteries, often with Romanesque, Gothic, and/or Mudéjar elements. In addition, the interaction between Spaniards and Indigenous people gave rise to artistic styles such as the tequitqui (from the Nahuatl: worker or builder). Years later, Baroque and Mannerist styles prevailed in large cathedrals and civil buildings, while in rural areas, haciendas or stately estates with Mozarabic tendencies were built.
In the 19th century, the neoclassical movement arose as the country gained independence and sought to establish itself as a republic. A famous example is the Hospicio Cabañas, an orphanage and hospital complex completed in 1829. The art nouveau, and the art deco were styles introduced into the design of the Palacio de Bellas Artes to mark the identity of the Mexican nation with Greek-Roman and pre-Columbian symbols.[citation needed]

As a new sense of nationalism developed in the 20th century, a strengthening central government issued formal policies that sought to use architecture to show Mexico's modernity and differentiation from other nations. The development of a Mexican modernist architecture was especially manifested in the mid-1950s construction of the Ciudad Universitaria, Mexico City, the main campus of the National Autonomous University of Mexico. Designed by the most prestigious architects of the era, including Mario Pani, Eugenio Peschard, and Enrique del Moral, the buildings feature murals by artists Diego Rivera, David Alfaro Siqueiros, and José Chávez Morado. It has since been recognized as a UNESCO World Heritage Site.[338]
Juan O'Gorman was one of the first environmental architects in Mexico, developing the "organic" theory, trying to integrate the building with the landscape within the same approaches of Frank Lloyd Wright.[339] In the search for a new architecture that does not resemble the styles of the past, it achieves a joint manifestation with the mural painting and the landscaping. Luis Barragán combined the shape of the space with forms of rural vernacular architecture of Mexico and Mediterranean countries (Spain-Morocco), integrating color that handles light and shade in different tones and opens a look at the international minimalism. He won the 1980 Pritzker Prize, the highest award in architecture.[340]
Cuisine

The origin of the current Mexican cuisine was established during the Spanish colonial era, a mixture of the foods of Spain with native indigenous ingredients.[342] Foods indigenous to Mexico include corn, pepper vegetables, calabazas, avocados, sweet potato, turkey, many beans, and other fruits and spices. Similarly, some cooking techniques used today are inherited from pre-Columbian peoples, such as the nixtamalization of corn, the cooking of food in ovens at ground level, grinding in molcajete and metate. With the Spaniards came the pork, beef and chicken meats; peppercorn, sugar, milk and all its derivatives, wheat and rice, citrus fruits and another constellation of ingredients that are part of the daily diet of Mexicans.
From this meeting of millennia old two culinary traditions, were born pozole, mole sauce, barbacoa and tamale in its current forms, chocolate, a large range of breads, tacos, and the broad repertoire of Mexican street foods. Beverages such as atole, champurrado, milk chocolate and aguas frescas were born; desserts such as acitrón and the full range of crystallized sweets, rompope, cajeta, jericaya and the wide repertoire of delights created in the convents of nuns in all parts of the country.
In 2005, Mexico presented the candidature of its gastronomy for World Heritage Site of UNESCO, the first time a country had presented its gastronomic tradition for this purpose.[343] The result was negative, because the committee did not place the proper emphasis on the importance of corn in Mexican cuisine.[344] On 16 November 2010 Mexican gastronomy was recognized as Intangible cultural heritage by UNESCO.[345] In addition, Daniela Soto-Innes was named the best female chef in the world by The World's Best 50 Restaurants in April 2019 and Elena Reygadas in 2023.[346]
Literature

Mexican literature has its antecedents in the literature of the indigenous settlements of Mesoamerica. Poetry had a rich cultural tradition in pre-Columbian Mexico, being divided into two broad categories—secular and religious. Aztec poetry was sung, chanted, or spoken, often to the accompaniment of a drum or a harp. While Tenochtitlan was the political capital, Texcoco was the cultural center; the Texcocan language was considered the most melodious and refined. The best well-known pre-Columbian poet is Nezahualcoyotl.[347]
There are historical chronicles of the conquest of Mexico by participants, and, later, by historians. Bernal Díaz del Castillo's True History of the Conquest of the New Spain is still widely read today. Spanish-born poet Bernardo de Balbuena extolled the virtues of Mexico in Grandeza mexicana (Mexican grandeur) (1604). Baroque literature flourished in the 17th century; the most notable writers of this period were Juan Ruiz de Alarcón and Juana Inés de la Cruz. Sor Juana was famous in her own time, called the "Ten Muse."[348]
The late colonial-era novel by José Joaquín Fernández de Lizardi, whose The Mangy Parrot ("El Periquillo Sarniento"), is said to be the first Latin American novel.[348] Nineteenth-century liberal of Nahua origin Ignacio Manuel Altamirano is an important writer of the era, along with Vicente Riva Palacio, the grandson of Mexican hero of independence Vicente Guerrero, who authored a series of historical novels as well as poetry. In the modern era, the novel of the Mexican Revolution by Mariano Azuela (Los de abajo, translated to English as The Underdogs) is noteworthy. Poet and Nobel Laureate Octavio Paz, novelist Carlos Fuentes, Alfonso Reyes, Renato Leduc, essayist Carlos Monsiváis, journalist and public intellectual Elena Poniatowska, and Juan Rulfo (Pedro Páramo), Martín Luis Guzmán, Nellie Campobello, (Cartucho).
Cinema

Mexican films from the Golden Age in the 1940s and 1950s are the greatest examples of Latin American cinema, with a huge industry comparable to the Hollywood of those years. Mexican films were exported and exhibited in all of Latin America and Europe. María Candelaria (1943) by Emilio Fernández, was one of the first films awarded a Palme d'Or at the Cannes Film Festival in 1946, the first time the event was held after World War II. The famous Spanish-born director Luis Buñuel realized in Mexico between 1947 and 1965 some of his masterpieces like Los Olvidados (1949) and Viridiana (1961). Famous actors and actresses from this period include María Félix, Pedro Infante, Dolores del Río, Jorge Negrete and the comedian Cantinflas.
More recently, films such as Como agua para chocolate (1992), Sex, Shame, and Tears (1999), Y tu mamá también (2001), and The Crime of Father Amaro (2002) have been successful in creating universal stories about contemporary subjects, and were internationally recognized. Mexican directors Alejandro González Iñárritu (Babel, Birdman, The Revenant, Bardo, False Chronicle of a Handful of Truths), Alfonso Cuarón (A Little Princess, Harry Potter and the Prisoner of Azkaban, Gravity, Roma), Guillermo del Toro (Pan's Labyrinth, Crimson Peak, The Shape of Water, Nightmare Alley), screenwriter Guillermo Arriaga and photographer Emmanuel Lubezki are some of the most known present-day film makers.
Music and dance

Mexico has a long tradition of music from the prehispanic era to the present. Much of the music from the colonial era was composed for religious purposes.[349][350]
Although the traditions of European opera and especially Italian opera had initially dominated the Mexican music conservatories and strongly influenced native opera composers (in both style and subject matter), elements of Mexican nationalism had already appeared by the latter part of the 19th century with operas such as Aniceto Ortega del Villar's 1871 Guatimotzin, a romanticized account of the defense of Mexico by its last Aztec ruler, Cuauhtémoc. The most well-known Mexican composer of the twentieth century is Carlos Chávez (1899–1978), who composed six symphonies with indigenous themes, and rejuvenated Mexican music, founding the Orquesta Sinfónica Nacional.[351]
Traditional Mexican music includes mariachi, banda, norteño, ranchera, and corridos. Corridos were particularly popular during the Mexican Revolution (1910–20) and in the present era include narcocorridos. The embrace of rock and roll by young Mexicans in the 1960s and 1970s brought Mexico into the transnational, counterculture movement of the era. In Mexico, the native rock culture merged into the larger countercultural and political movement of the late 1960s, culminating in the 1968 protests and redirected into counterculture rebellion, La Onda (the wave).[352][353]
On an everyday basis most Mexicans listen to contemporary music such as pop, rock, and others in both English and Spanish. Folk dance of Mexico along with its music is both deeply regional and traditional. Founded in 1952, the Ballet Folklórico de México performs music and dance of the prehispanic period through the Mexican Revolution in regional attire in the Palacio de Bellas Artes.[354]
Media

There was a major reform of the telecommunications industry in 2013, with the creation of new broadcast television channels. There had been a longstanding limitation on the number of networks, with Televisa, with a virtual monopoly; TV Azteca, and Imagen Television. New technology has allowed the entry of foreign satellite and cable companies. Mexico became the first Latin American country to transition from analog to all digital transmissions.[355]
Telenovelas, or soap operas are very traditional in Mexico and are translated to many languages and seen all over the world. Mexico was a pioneer in edutainment, with TV producer Miguel Sabido creating in 1970s "soap operas for social change". The "Sabido method" has been adopted in many other countries subsequently, including India, Peru, Kenya, and China.[356] The Mexican government successfully used a telenovela to promote family planning in the 1970s to curb the country's high birth rate.[357]
Bilingual government radio stations broadcasting in Spanish and indigenous languages were a tool for indigenous education (1958–65) and since 1979 the Instituto Nacional Indigenista has established a national network of bilingual radio stations.[358]
Sports

Organized sport in Mexico largely dates from the late nineteenth century, with only bullfighting having a long history dating to the early colonial era. Once the political turmoil of the early republic was replaced by the stability of the Porfiriato did organized sport become public diversions, with structured and ordered play governed by rules and authorities. Baseball was introduced from the United States and also via Cuba in the 1880s and organized teams were created. After the Mexican Revolution, the government sponsored sports to counter the international image of political turmoil and violence.[359]
The bid to host the 1968 Summer Olympics was to burnish Mexico's stature internationally, with is being the first Latin American country to host the games. The government spent abundantly on sporting facilities and other infrastructure to make the games a success, but those expenditures helped fuel public discontent with the government's lack of spending on social programs.[359] Mexico City hosted the XIX Olympic Games in 1968, making it the first Latin American city to do so.[360] The country has also hosted the FIFA World Cup twice, in 1970 and 1986.[361] With its past hosting of the 1970 and 1986 tournaments, Mexico will become the first country to host or co-host the men's World Cup three times. When it the 2026 FIFA World Cup will be jointly hosted by 16 cities in three North American countries: Canada, Mexico, and the United States. Mexico's most popular sport is association football.

The Mexican professional baseball league is named the Liga Mexicana de Beisbol. While usually not as strong as the United States, the Caribbean countries and Japan, Mexico has nonetheless achieved several international baseball titles.[362][363]
Other sporting activities include Bullfighting, boxing, and Lucha Libre (freestyle professional wrestling). Bullfighting (Spanish: corrida de toros) came to Mexico 500 years ago with the arrival of the Spanish. Despite efforts by animal rights activists to outlaw it, bullfighting remains a popular sport in the country, and almost all large cities have bullrings. Plaza México in Mexico City, which seats 45,000 people, is the largest bullring in the world.[364] Freestyle professional wrestling is a major crowd draw with national promotions such as AAA, CMLL and others.[365]
Mexico is an international power in professional boxing.[365] Thirteen Olympic boxing medals have been won by Mexico.[366]
See also
- Index of Mexico-related articles
- Outline of Mexico
- Mexican War of Independence
Notes
- ^ Spanish: México or Méjico, pronunciation: [ˈmexiko] ; Classical Nahuatl: Mēxihco; Yucatec Maya: Meejikoo
- ^ Usually, in Spanish, the name of the country is spelled México; however, in Peninsular (European) Spanish, the variant Méjico is used alongside the usual version. According to the Diccionario panhispánico de dudas by the Royal Spanish Academy and Association of Academies of the Spanish Language, the version with J is also correct; however, the spelling with X is recommended, as it is the one used in Mexico.[10]
- ^ Spanish: Estados Unidos Mexicanos ([esˈtaðos uˈniðos mexiˈkanos] ); Classical Nahuatl: Mēxihcatl Tlacetilīlli Tlahtohcāyōtl
References
- ^ "Global Religion - Religious Beliefs Across the World" (PDF). Ipsos. May 2023. Archived (PDF) from the original on 12 May 2023. Retrieved 23 August 2023.
- ^ "Political Constitution of the United Mexican States, title 2, article 40" (PDF). MX Q: SCJN. Archived from the original (PDF) on 11 May 2011. Retrieved 14 August 2010.
- ^ "Surface water and surface water change". Organisation for Economic Co-operation and Development (OECD). Archived from the original on 24 March 2021. Retrieved 11 October 2020.
- ^ "Mexico". The World Factbook (2024 ed.). Central Intelligence Agency. Retrieved 22 June 2023.
- ^ a b c d "World Economic Outlook Database, April 2024 Edition. (Mexico)". www.imf.org. International Monetary Fund. 16 April 2024. Retrieved 16 April 2024.
- ^ Inequality - Income inequality - OECD Data. OECD. Archived from the original on 1 July 2022. Retrieved 12 August 2021.
- ^ "Human Development Report 2023/24" (PDF). United Nations Development Programme. 13 March 2024. Archived (PDF) from the original on 13 March 2024. Retrieved 13 March 2024.
- ^ INALI (13 March 2003). "General Law of Linguistic Rights of the Indigenous Peoples" (PDF). Archived (PDF) from the original on 3 August 2016. Retrieved 7 November 2010.
- ^ "Catálogo de las lenguas indígenas nacionales: Variantes lingüísticas de México con sus autodenominaciones y referencias geoestadísticas". Inali.gob.mx. Archived from the original on 8 July 2014. Retrieved 18 July 2014.
- ^ México in Diccionario panhispánico de dudas by Royal Spanish Academy and Association of Academies of the Spanish Language, Madrid: Santillana. 2005. ISBN 978-8-429-40623-8.
- ^ a b "Mexico". The World Factbook. Central Intelligence Agency. Archived from the original on 26 January 2021.
- ^ a b c d e f g "Censo Población y Vivienda 2020". www.inegi.org.mx. INEGI. Archived from the original on 14 February 2022. Retrieved 26 January 2021.
- ^ Merriam-Webster's Geographical Dictionary, 3rd ed., Springfield, Massachusetts, United States, Merriam-Webster; p. 733
- ^ Brading, D.A., The First America: The Spanish Monarchy, Creole Patriots, and the Liberal State. Cambridge: Cambridge University Press 1991. ISBN 052139130X
- ^ Ricard, Robert, The Spiritual Conquest of Mexico, Lesley Byrd Simpson, trans. Berkeley and Los Angeles: University of California Press 1966
- ^ Greenberg, Amy S. (2013). A wicked war : Polk, Clay, Lincoln, and the 1846 U.S. invasion of Mexico. New York. ISBN 978-0-307-47599-2. OCLC 818318029. Archived from the original on 21 February 2024. Retrieved 5 March 2022.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Garner, Paul. Porfirio Díaz. Routledge 2001.
- ^ Paweł Bożyk (2006). "Newly Industrialized Countries". Globalization and the Transformation of Foreign Economic Policy. Ashgate Publishing. p. 164. ISBN 978-0-7546-4638-9. Archived from the original on 4 November 2023. Retrieved 23 July 2018.
- ^ [1] Archived 4 February 2024 at the Wayback Machine UNESCO World Heritage sites, accessed 9 May 2022
- ^ "What is a mega-diverse country?". Mexican biodiversity. Archived from the original on 7 September 2019. Retrieved 13 July 2019.
- ^ "México ocupa el sexto lugar en turismo a nivel mundial". www.expansion.mx. CNN Expansión. 28 August 2018. Archived from the original on 23 December 2019. Retrieved 8 January 2019.
- ^ James Scott; Matthias vom Hau; David Hulme. "Beyond the BICs: Strategies of influence". The University of Manchester. Archived from the original on 25 May 2017. Retrieved 11 April 2012.
- ^ Nolte, Detlef (October 2010). "How to compare regional powers: analytical concepts and research topics". Review of International Studies. 36 (4): 881–901. doi:10.1017/S026021051000135X. ISSN 0260-2105. JSTOR 40961959. S2CID 13809794. ProQuest 873500719. Archived from the original on 2 March 2021. Retrieved 17 November 2020.
- ^ "Oxford Analytica". Archived from the original on 24 April 2007. Retrieved 17 July 2013.
- ^ "G8: Despite Differences, Mexico Comfortable as Emerging Power". ipsnews.net. 5 June 2007. Archived from the original on 16 August 2008. Retrieved 30 May 2010.
- ^ Mauro F. Guillén (2003). "Multinationals, Ideology, and Organized Labor". The Limits of Convergence. Princeton University Press. p. 126 (table 5.1). ISBN 978-0-691-11633-4. Archived from the original on 21 February 2024. Retrieved 23 July 2018.
- ^ David Waugh (2000). "Manufacturing industries (chapter 19), World development (chapter 22)". Geography, An Integrated Approach (3rd ed.). Nelson Thornes. pp. 563, 576–579, 633, and 640. ISBN 978-0-17-444706-1. Archived from the original on 4 February 2024. Retrieved 23 July 2018.
- ^ N. Gregory Mankiw (2007). Principles of Economics (4th ed.). Mason, Ohio: Thomson/South-Western. ISBN 978-0-324-22472-6. Archived from the original on 4 February 2024. Retrieved 23 July 2018.
- ^ "Global Peace Index 2019: Measuring Peace in a Complex World" (PDF). Vision of Humanity. Sydney: Institute for Economics & Peace. June 2019. Archived from the original (PDF) on 27 August 2019. Retrieved 4 June 2020.
- ^ a b Brianna Lee; Danielle Renwick; Rocio Cara Labrador (24 January 2019). "Mexico's Drug War". Council on Foreign Relations. Archived from the original on 16 July 2019. Retrieved 19 July 2019.
- ^ William Bright (2004). Native American Placenames of the United States. University of Oklahoma Press. p. 281. ISBN 978-0-8061-3598-4.
- ^ "El cambio de la denominación de "Estados Unidos Mexicanos" por la de "México" en la Constitución Federal". ierd.prd.org.mx. Archived from the original on 1 November 2008. Retrieved 4 November 2009.
- ^ "Constitución Mexicana de 1857". www.tlahui.com. Archived from the original on 5 October 2018. Retrieved 30 May 2010.
- ^ "Leyes Constitucionales de 1836". Cervantesvirtual.com. 29 November 2010. Archived from the original on 23 August 2013. Retrieved 17 July 2013.
- ^ Werner 2001, pp. 386–.
- ^ Susan Toby Evans; David L. Webster (2013). Archaeology of Ancient Mexico and Central America: An Encyclopedia. Routledge. p. 54. ISBN 978-1-136-80186-0.
- ^ Colin M. MacLachlan (13 April 2015). Imperialism and the Origins of Mexican Culture. Harvard University Press. p. 39. ISBN 978-0-674-28643-6.
- ^ Carmack, Robert M.; Gasco, Janine L.; Gossen, Gary H. (2016). The Legacy of Mesoamerica: History and Culture of a Native American Civilization. Routledge. ISBN 978-1-317-34678-4.[page needed]
- ^ Diehl, Richard A. (2004). The Olmecs: America's First Civilization. Thames & Hudson. pp. 9–25. ISBN 978-0-500-02119-4.
- ^ Restall, Matthew, "A History of the New Philology and the New Philology in History", Latin American Research Review - Volume 38, Number 1, 2003, pp.113–134
- ^ Sampson, Geoffrey (1985). Writing Systems: A Linguistic Introduction. Stanford University Press. ISBN 978-0-8047-1756-4.[page needed]
- ^ Cowgill, George L. (21 October 1997). "State and Society at Teotihuacan, Mexico". Annual Review of Anthropology. 26 (1): 129–161. doi:10.1146/annurev.anthro.26.1.129. OCLC 202300854. S2CID 53663189.
- ^ "Ancient Civilizations of Mexico". Ancient Civilizations World. 12 January 2017. Archived from the original on 12 July 2019. Retrieved 14 July 2019.
- ^ "The word "Azteca" was NOT created by Von Humboldt!". Mexicka.org. 31 May 2014. Archived from the original on 25 March 2019. Retrieved 13 July 2019.
- ^ León Portilla, Miguel (10 May 2009). "Los aztecas, disquisiciones sobre un gentilico". Estudios de Cultura Náhuatl. 31 (31). Archived from the original on 21 December 2020. Retrieved 17 November 2020.
- ^ Lockhart, James and Stuart B. Schwartz. Early Latin America. Cambridge: Cambridge University Press 1983, 59
- ^ Chuchiak, John F. IV, "Inquisition" in Encyclopedia of Mexico. Chicago: Fitzroy Dearborn 1997, pp. 704–708
- ^ Schmal, John P. (17 July 2003). "The Indigenous People of Zacatecas". Latino LA: Comunidad. Archived from the original on 14 March 2016. Retrieved 14 July 2019.
- ^ Charlotte M. Gradie (2000). "The Tepehuan Revolt of 1616: Militarism, Evangelism, and Colonialism in Seventeenth-Century Nueva Vizcaya". The Americas. 58 (2). Salt Lake City: University of Utah Press: 302–303. doi:10.1353/tam.2001.0109. S2CID 144896113.
- ^ Wasserstrom, Robert (1980). "Ethnic Violence and Indigenous Protest: The Tzeltal (Maya) Rebellion of 1712". Journal of Latin American Studies. 12: 1–19. doi:10.1017/S0022216X00017533. S2CID 145718069.
- ^ Taylor, William B. (1 June 1979). Drinking, Homicide, and Rebellion in Colonial Mexican Villages (1st ed.). Stanford: Stanford University Press. ISBN 978-0804711128.
- ^ White, Benjamin (31 January 2017). "Campeche, Mexico – largest pirate attack in history, now UNESCO listed". In Search of Lost Places. Archived from the original on 15 July 2019. Retrieved 14 July 2019.
- ^ Knispel, Sandra (13 December 2017). "The mysterious aftermath of an infamous pirate raid". University of Rochester Newsletter. Archived from the original on 15 July 2019. Retrieved 14 July 2019.
- ^ Cope, R. Douglas (1994). The Limits of Racial Domination: Plebeian Society in Colonial Mexico City, 1660–1720. Madison, Wis.: University of Wisconsin.
- ^ Altman, et al. The Early History of Greater Mexico, 342–43
- ^ "Grito de Dolores". Encyclopaedia Britannica. Archived from the original on 11 September 2018. Retrieved 12 September 2018.
- ^ Van Young, Stormy Passage, 179–226
- ^ Benson, Nettie Lee (February 1945). "The Plan of Casa Mata". Hispanic American Historical Review. 25: 45–56. doi:10.1215/00182168-25.1.45.
- ^ Hale, Charles A. (1968). Mexican Liberalism in the Age of Mora. New Haven: Yale University Press. p. 224.
- ^ "Ways of ending slavery". Encyclopædia Britannica. Archived from the original on 16 October 2014. Retrieved 23 June 2022.
- ^ Costeloe, Michael P. "Pastry War". Encyclopedia of Latin American History and Culture. Vol. 4. p. 318.
- ^ Van Young, Stormy Passage, "The Age of Santa Anna", 227–270
- ^ Weber, David J., The Mexican Frontier, 1821–1846: The American Southwest under Mexico, University of New Mexico Press, 1982
- ^ Angel Miranda Basurto (2002). La Evolucíon de Mėxico [The Evolution of Mexico] (in Spanish) (6th ed.). Mexico City: Editorial Porrúa. p. 358. ISBN 970-07-3678-4.
- ^ Britton, John A. "Liberalism". Encyclopedia of Mexico. p. 739.
- ^ Hamnett, Brian. "Benito Juárez". Encyclopedia of Mexico. pp. 719–20.
- ^ Britton, "Liberalism" p. 740.
- ^ Sullivan, Paul. "Sebastián Lerdo de Tejada". Encyclopedia of Mexico. pp. 736–38.
- ^ Adela M. Olvera (2 February 2018). "El Porfiriato en Mexico" [The Porfirio Era in Mexico]. Inside Mexico.com (in Spanish). Archived from the original on 26 March 2019. Retrieved 18 July 2019.
- ^ Buchenau, Jürgen. "Científicos". Encyclopedia of Mexico. pp. 260–265.
- ^ Schmidt, Arthur. "José Ives Limantour". Encyclopedia of Mexico. pp. 746–49.
- ^ "cientifico". Encyclopædia Britannica. Archived from the original on 7 February 2017. Retrieved 7 February 2017.
- ^ Brenner, Anita (1 January 1984). The Wind that Swept Mexico: The History of the Mexican Revolution of 1910–1942 (New ed.). University of Texas Press. ISBN 978-0292790247.
- ^ Benjamin, Thomas. La Revolución: Mexico's Great Revolution as Memory, Myth, and History. Austin: University of Texas Press 2000
- ^ a b c Matute, Alvaro. "Mexican Revolution: May 1917 – December 1920" in Encyclopedia of Mexico, 862–864.
- ^ "The Mexican Revolution". Public Broadcasting Service. 20 November 1910. Archived from the original on 14 May 2011. Retrieved 17 July 2013.
- ^ Robert McCaa. "Missing millions: the human cost of the Mexican Revolution". University of Minnesota Population Center. Archived from the original on 2 April 2016. Retrieved 17 July 2013.
- ^ Katz, Friedrich. The Secret War in Mexico. Chicago: University of Chicago Press.
- ^ "The Mexican Revolution and the United States in the Collections of the Library of Congress, U.S. Involvement Before 1913". Library of Congress. Archived from the original on 19 July 2019. Retrieved 18 July 2019.
- ^ "Punitive Expedition in Mexico, 1916–1917". U.S. Department of State archive. 20 January 2009. Archived from the original on 15 June 2023. Retrieved 18 July 2019.
- ^ "ZIMMERMANN TELEGRAM". The National WWI Museum and Memorial. 2 March 2017. Archived from the original on 19 July 2019. Retrieved 18 July 2019.
- ^ Rafael Hernández Ángeles. "85º Aniversario de la Fundación del Partido Nacional Revolucionario (PNR)" [85th anniversary of the founding of the National Revolutionary Party (PRN)]. Instituto Nacional de Estudios Historicos de las Revoluciones de Mexico (in Spanish). Archived from the original on 19 July 2019. Retrieved 18 July 2019.
- ^ "The Mexican Miracle: 1940–1968". World History from 1500. Emayzine. Archived from the original on 3 April 2007. Retrieved 30 September 2007.
- ^ Staff, M. N. D. (13 March 2024). "He left India for Mexico to solve global hunger: Meet Ravi Singh". Mexico News Daily. Archived from the original on 14 March 2024. Retrieved 14 March 2024.
...specifically the Yaqui Valley in Sonora... is considered the birthplace of the Green Revolution.
- ^ Elena Poniatowska (1975). Massacre in Mexico. Viking, New York. ISBN 978-0-8262-0817-0. Archived from the original on 4 February 2024. Retrieved 23 July 2018.
- ^ Kennedy, Duncan (19 July 2008). "Mexico's long forgotten dirty war". BBC News. Archived from the original on 29 June 2017. Retrieved 17 July 2013.
- ^ Krauze, Enrique (January–February 2006). "Furthering Democracy in Mexico". Foreign Affairs. Archived from the original on 10 January 2006. Retrieved 7 October 2007.
- ^ Schedler, Andreas (2006). Electoral Authoritarianism: The Dynamics of Unfree Competition. L. Rienner Publishers. ISBN 978-1-58826-440-4. Archived from the original on 4 February 2024. Retrieved 23 July 2018.
- ^ Crandall, R.; Paz and Roett (2004). "Mexico's Domestic Economy: Policy Options and Choices". Mexico's Democracy at Work. Lynne Reinner Publishers. p. 160. ISBN 978-0-8018-5655-6.
- ^ ""Mexico The 1988 Elections" (Sources: The Library of the Congress Country Studies, CIA World Factbook)". Photius Coutsoukis. Archived from the original on 15 September 2018. Retrieved 30 May 2010.
- ^ Gomez Romero, Luis (5 October 2018). "Massacres, disappearances and 1968: Mexicans remember the victims of a 'perfect dictatorship'". The Conversation. Archived from the original on 12 May 2019. Retrieved 12 May 2019.
- ^ "Vargas Llosa: "México es la dictadura perfecta"". El País. 1 September 1990. Archived from the original on 24 October 2011. Retrieved 12 May 2019.
- ^ Reding, Andrew (1991). "Mexico: The Crumbling of the "Perfect Dictatorship"". World Policy Journal. 8 (2): 255–284. JSTOR 40209208.
- ^ Cruz Vasconcelos, Gerardo. "Desempeño Histórico 1914–2004" (PDF) (in Spanish). Archived from the original (PDF) on 3 July 2006. Retrieved 17 February 2007.
- ^ Valles Ruiz, Rosa María (June 2016). "Elecciones presidenciales 2006 en México. La perspectiva de la prensa escrita" [2006 presidential Elections in Mexico. The Perspective of the Press]. Revista mexicana de opinión pública (in Spanish) (20): 31–51. Archived from the original on 21 March 2020. Retrieved 12 July 2019.
- ^ Reséndiz, Francisco (2006). "Rinde AMLO protesta como "presidente legítimo"". El Universal (in Spanish). Archived from the original on 18 January 2012. Retrieved 1 October 2007.
- ^ "Enrique Pena Nieto wins Mexican presidential election". The Telegraph. 2 July 2012. Archived from the original on 10 January 2022. Retrieved 25 August 2015.
- ^ Sieff, Kevin. "López Obrador, winner of Mexican election, given broad mandate". Washington Post. Archived from the original on 2 July 2018. Retrieved 2 July 2018.
- ^ Sharma, Gaurav (10 May 2018). "Mexico's Oil And Gas Industry Privatization Efforts Nearing Critical Phase". Forbes. Archived from the original on 4 June 2020. Retrieved 4 June 2020.
- ^ Barrera Diaz, Cyntia; Villamil, Justin; Still, Amy (14 February 2020). "Pemex Ex-CEO Arrest Puts AMLO in Delicate Situation". Rigzone. Bloomberg. Archived from the original on 27 May 2020. Retrieved 4 June 2020.
- ^ "Mexico's presidential front runner on high alert for election fraud ahead of Sunday's vote". South China Morning Post. Associated Press. 30 June 2018. Archived from the original on 23 May 2020. Retrieved 4 June 2020.
- ^ "Mexico's 2018 Elections: Results and Potential Implications" (PDF). fas.org. 17 July 2018. Archived (PDF) from the original on 4 February 2024. Retrieved 12 April 2021.
- ^ "Mexico's López Obrador sworn in as first leftist president in decades". BBC News. 2 December 2018. Archived from the original on 14 April 2021. Retrieved 7 April 2021.
- ^ "Ruling leftist party candidate Sheinbaum elected Mexico's first female president". 3 June 2024. Archived from the original on 3 June 2024. Retrieved 3 June 2024.
- ^ "Nord-Amèrica, in Gran Enciclopèdia Catalana". Grec.cat. Archived from the original on 15 May 2016. Retrieved 17 July 2013.
- ^ Parsons, Alan; Jonathan Schaffer (May 2004). Geopolitics of oil and natural gas. Economic Perspectives. U.S. Department of State.
- ^ Vargas, Jorge A. (2011). Mexico and the Law of the Sea: Contributions and Compromises. Martinus Nijhoff Publishers. p. 405. ISBN 9789004206205. Archived from the original on 4 February 2024. Retrieved 25 September 2020.
- ^ Fact Book Archived 13 October 2023 at the Wayback Machine Mexico. Accessed 4 May 2022
- ^ [2] [dead link] Mexico Fact Book. accessed 6 May 2022
- ^ [3] [dead link] Mexico Fact Book. accessed 5 May 2022
- ^ a b "Drainage". Encyclopedia Britannica Mexico. Archived from the original on 1 July 2022. Retrieved 6 May 2022.
- ^ "Ocupa México cuarto lugar mundial de biodiversidad". El Economista (in Spanish). Archived from the original on 6 February 2017. Retrieved 5 February 2017.
- ^ a b "Biodiversidad de México". SEMARNAT. Archived from the original on 7 October 2007. Retrieved 7 October 2007.
- ^ "Biodiversidad en México". CONEVYT. Archived from the original on 7 October 2007. Retrieved 7 October 2007.
- ^ a b "Sistema Nacional sobre la Biodiversidad en México". CONABIO. Archived from the original on 12 October 2007. Retrieved 7 October 2007.
- ^ "Mexico's 'devastating' forest loss". BBC News. 4 March 2002. Archived from the original on 16 January 2018. Retrieved 8 August 2011.
- ^ Grantham, H. S.; Duncan, A.; Evans, T. D.; Jones, K. R.; Beyer, H. L.; Schuster, R.; Walston, J.; Ray, J. C.; Robinson, J. G.; Callow, M.; Clements, T.; Costa, H. M.; DeGemmis, A.; Elsen, P. R.; Ervin, J.; Franco, P.; Goldman, E.; Goetz, S.; Hansen, A.; Hofsvang, E.; Jantz, P.; Jupiter, S.; Kang, A.; Langhammer, P.; Laurance, W. F.; Lieberman, S.; Linkie, M.; Malhi, Y.; Maxwell, S.; Mendez, M.; Mittermeier, R.; Murray, N. J.; Possingham, H.; Radachowsky, J.; Saatchi, S.; Samper, C.; Silverman, J.; Shapiro, A.; Strassburg, B.; Stevens, T.; Stokes, E.; Taylor, R.; Tear, T.; Tizard, R.; Venter, O.; Visconti, P.; Wang, S.; Watson, J. E. M. (8 December 2020). "Anthropogenic modification of forests means only 40% of remaining forests have high ecosystem integrity". Nature Communications. 11 (1): 5978. Bibcode:2020NatCo..11.5978G. doi:10.1038/s41467-020-19493-3. PMC 7723057. PMID 33293507.
- ^ "SGI 2022 | Mexico | Environmental Policies". Archived from the original on 18 April 2024. Retrieved 18 April 2024.
- ^ Hayden, Cori. 2003. When Nature Goes Public: The Making and Unmaking of Bioproscpecting in Mexico. Princeton University Press.
- ^ Laveaga, Gabriela Soto (2009). Jungle Laboratories: Mexican Peasants, National Projects, and the Making of the Pill. Duke University Press. ISBN 978-0-8223-9196-8.[page needed]
- ^ "Articles 50 to 79". Political Constitution of the United Mexican States. Congress of the Union of the United Mexican States. Archived from the original on 13 November 2006. Retrieved 3 October 2007.
- ^ "Third Title, First Chapter, About Electoral systems" (PDF). Código Federal de Instituciones y Procedimientos Electorales (Federal Code of Electoral Institutions and Procedures) (in Spanish). Congress of the Union of the United Mexican States. 15 August 1990. Archived from the original (PDF) on 25 October 2007. Retrieved 3 October 2007.
- ^ a b "Third Title, First Chapter, About Electoral systems, Article 11–1" (PDF). Código Federal de Instituciones y Procedimientos Electorales (Federal Code of Electoral Institutions and Procedures) (in Spanish). Congress of the Union of the United Mexican States. 15 August 1990. Archived from the original (PDF) on 25 October 2007. Retrieved 3 October 2007.
- ^ "Fourth Title, Second Chapter, About coalitions, Article 59–1" (PDF). Código Federal de Instituciones y Procedimientos Electorales (Federal Code of Electoral Institutions and Procedures) (in Spanish). Congress of the Union of the United Mexican States. 15 August 1990. Archived from the original (PDF) on 25 October 2007. Retrieved 3 October 2007.
- ^ "Articles 80 to 93". Political Constitution of the United Mexican States. Congress of the Union of the United Mexican States. Archived from the original on 13 November 2006. Retrieved 3 October 2007.
- ^ "Articles 90 to 107". Political Constitution of the United Mexican States. Congress of the Union of the United Mexican States. Archived from the original on 13 November 2006. Retrieved 3 October 2007.
- ^ Niko Vorobyov, ed. (2019). Dopeworld: Adventures in Drug Lands. Hachette UK. ISBN 9781317755098. Archived from the original on 1 April 2023. Retrieved 19 January 2021.
... Mexico spent most of the twentieth century governed by the Institutional Revolutionary Party or PRI, a bigtent, catch-all alliance that included everyone ...
- ^ "Entrevista a la Lic. Beatriz Paredes Rangel, Presidenta dle Comité Ejecutivo Nacional del PRI". 17 December 2008. Archived from the original on 17 December 2008. Retrieved 17 July 2013.
- ^ "Miembros Titulares". ODCA. 14 July 2008. Archived from the original on 14 July 2008. Retrieved 17 July 2013.
- ^ "Estatuto del Partido de la Revolución Democrática" (PDF). Archived from the original (PDF) on 16 January 2013. Retrieved 17 July 2013.
- ^ a b Political Constitution of the United Mexican States (5 February 1917). "Article 89, Section 10" (PDF) (in Spanish). Chamber of Deputies. Archived from the original (PDF) on 25 August 2007. Retrieved 28 March 2009.
- ^ Internal Rules of the Ministry of Foreign Affairs (10 August 2001). "Article 2, Section 1" (in Spanish). Ministry of Foreign Affairs. Archived from the original on 11 June 2008. Retrieved 28 March 2009.
- ^ Palacios Treviño, Jorge. "La Doctrina Estrada y el Principio de la No-Intervención" (PDF) (in Spanish). Archived from the original (PDF) on 6 February 2009. Retrieved 4 April 2009.
- ^ UN (7 November 1945). "United Nations Member States". UN official website. Archived from the original on 17 April 2009. Retrieved 6 April 2009.
- ^ Velázquez Flores (2007), p. 145.
- ^ Organization of Ibero-American States. "Members" (in Spanish). OEI official website. Archived from the original on 16 December 2022. Retrieved 6 April 2009.
- ^ OPANAL. "Members". OPANAL official website. Archived from the original on 14 August 2009. Retrieved 6 April 2009.
- ^ Ministry of Foreign Affairs (7 March 2007). "El Presidente Felipe Calderón Hinojosa en la Ceremonia de Entrega de la Secretaría Pro Témpore del Grupo de Río" (in Spanish). Gobierno Federal. Archived from the original on 23 August 2009. Retrieved 6 April 2009.
- ^ United Nations (2008). "Regular Budget Payments of Largest Payers". Global Policy. Archived from the original on 16 December 2022. Retrieved 4 April 2009.
- ^ Organisation for Economic Co-operation and Development (18 May 1994). "Members". OECD official website. Archived from the original on 5 February 2012. Retrieved 6 April 2009.
- ^ "Chile joins the OECD's Economic Club". BBC News. 12 January 2010. Archived from the original on 9 February 2010. Retrieved 23 April 2010.
- ^ "Japan's Regional Diplomacy, Latin America and the Caribbean" (PDF). Ministry of Foreign Affairs of Japan. Archived (PDF) from the original on 16 March 2023. Retrieved 4 April 2009.
- ^ "Latin America: Region is losing ground to competitors". Oxford Analytica. Archived from the original on 24 October 2007. Retrieved 4 April 2009.
- ^ Ministry of Foreign Affairs (2005), p. 215.
- ^ Maggie Farley (22 July 2005). "Mexico, Canada Introduce Third Plan to Expand Security Council". Los Angeles Times. Archived from the original on 6 December 2010. Retrieved 4 April 2009.
- ^ [4] [dead link] World Fact Book, Mexico. accessed 4 May 2022
- ^ Loke. "Capacitarán a militares en combates con rifles láser | Ediciones Impresas Milenio". Impreso.milenio.com. Archived from the original on 14 May 2010. Retrieved 30 May 2010.
- ^ "Strategy on recent equipment purchases: The Mexican Armed Forces in Transition" (PDF). Archived from the original (PDF) on 25 January 2017. Retrieved 17 July 2013.
- ^ "Text of the Treaty of Tlatelolco". Opanal.org. 27 November 1963. Archived from the original on 30 April 2011. Retrieved 9 March 2011.
- ^ "Chapter XXVI: Disarmament – No. 9 Treaty on the Prohibition of Nuclear Weapons". United Nations Treaty Collection. 7 July 2017. Archived from the original on 6 August 2019. Retrieved 9 August 2019.
- ^ Gustavo Iruegas (27 April 2007). "Adiós a la neutralidad". La Jornada (in Spanish). Archived from the original on 27 February 2018. Retrieved 4 April 2009.
- ^ Ricardo Gómez & Andrea Merlos (20 April 2007). "Diputados, en Favor de Derogar Neutralidad en Guerras". El Universal (in Spanish). Archived from the original on 15 October 2013. Retrieved 4 April 2009.
- ^ "A Look At Mexico's New National Guard". NPR. 13 July 2019. Archived from the original on 28 June 2022. Retrieved 14 May 2022.
- ^ [5] [dead link] World Fact Book accessed 14 May 2022.
- ^ "Big, expensive and weirdly spineless". The Economist. 14 February 2008. Archived from the original on 21 April 2008. Retrieved 17 July 2013.
- ^ a b c "Mexico". Britannica Online Encyclopedia. Archived from the original on 17 March 2011. Retrieved 6 March 2011.
- ^ "A Woman's Haunting Disappearance Sparks Outrage in Mexico Over Gender Violence" Archived 17 May 2022 at the Wayback Machine New York Times accessed 17 May 2022.
- ^ "Same-Sex Marriage Around the World". Pew Research Center. Archived from the original on 16 January 2023. Retrieved 11 September 2023.
- ^ International Gay and Lesbian Human Rights Commission (23 April 2003). "Mexico protects its gay and lesbian citizens with new law". Archived from the original on 21 February 2014. Retrieved 27 November 2009.
- ^ "STONEWALL GLOBAL WORKPLACE BRIEFINGS 2018 MEXICO" (PDF). Stonewall. Archived (PDF) from the original on 4 October 2023. Retrieved 11 September 2023.
- ^ Lopez, Oscar. "Mexico sees deadliest year for LGBT+ people in five years". Reuters. Archived from the original on 4 October 2023. Retrieved 11 September 2023.
- ^ "Mexico: Events of 2021". World Report, Mexico 2022. Human Rights Watch. 10 December 2021. Archived from the original on 12 August 2022. Retrieved 14 May 2022 – via Human Rights Watch.org.
- ^ "Mexico crime and violence in numbers" Archived 8 May 2022 at the Wayback Machine BBC News, accessed 8 May 2022
- ^ "Mexico disappearances reach record high of 100,000 amid impunity" Archived 8 January 2024 at the Wayback Machine BBC News accessed 17 May 2022.
- ^ [6] Archived 14 August 2022 at the Wayback Machine "In Mexico, One Cartel Is Cleared, but Others Storm In" New York Times, accessed 8 May 2022
- ^ [7] Archived 27 May 2022 at the Wayback Machine "How Mexico's Cartels Have Learned Military Tactics", accessed 8 May 2022
- ^ Franco, Yanira (1 October 2015). "Uno de cada cinco, víctima de algún delito: Inegi" [One in five, victim of a crime: Inegi]. Milenio (in Spanish). Mexico City. Archived from the original on 4 June 2020. Retrieved 4 June 2020.
- ^ Tuckman, Jo (21 November 2014). "Mexicans in biggest protest yet over missing students". The Guardian. Mexico City. Archived from the original on 8 May 2020. Retrieved 4 June 2020.
- ^ "Freedom of Expression in Mexico". PEN American Center. Archived from the original on 23 July 2013.
- ^ Alcázar, Jesús (17 July 2014). "Más de 100 periodistas asesinados en México desde el año 2000" (in Spanish). El Mundo (Spain). EFE. Archived from the original on 24 September 2015. Retrieved 3 March 2018.
- ^ a b Amanda Briney (8 October 2018). "Mexico's 31 States and One Federal District". Thought.Co. Archived from the original on 15 July 2019. Retrieved 15 July 2019.
- ^ "Article 116". Political Constitution of the United Mexican States. Congress of the Union of the United Mexican States. Archived from the original on 13 November 2006. Retrieved 7 October 2007.
- ^ "Article 112". Political Constitution of the United Mexican States. Congress of the Union of the United Mexican States. Archived from the original on 13 November 2006. Retrieved 7 October 2007.
- ^ "Federal District is now officially Mexico City: The change brings more autonomy for the country's capital". Mexico News Daily. 30 January 2016. Archived from the original on 21 July 2017. Retrieved 5 January 2018.
- ^ "Article 115". Political Constitution of the United Mexican States. Congress of the Union of the United Mexican States. Archived from the original on 13 November 2006. Retrieved 7 October 2007.
- ^ a b c Caleb Silver (7 June 2019). "Top 20 Economies in the World". Investopedia.com. Archived from the original on 17 July 2021. Retrieved 15 July 2019.
- ^ "Total GNI Atlas Method 2009, World Bank" (PDF). Archived from the original (PDF) on 5 November 2010. Retrieved 27 December 2010.
- ^ Andrew Jacobs; Matt Richtel (11 December 2017). "A Nasty, Nafta-Related Surprise: Mexico's Soaring Obesity". The New York Times. Archived from the original on 12 December 2017. Retrieved 12 December 2017.
- ^ "GNI per capita 2009, Atlas method and PPP, World Bank" (PDF). Archived (PDF) from the original on 9 September 2019. Retrieved 27 December 2010.
- ^ "Reporte ECLAC" (PDF) (in Spanish). Archived from the original (PDF) on 15 June 2007. Retrieved 16 February 2007.
- ^ Hufbauer, G.C.; Schott, J.J. (1 January 2005), "Chapter 1, Overview" (PDF), NAFTA Revisited: Achievements and Challenges, Washington, DC: Institute for International Economics (published October 2005), pp. 1–78, ISBN 978-0-88132-334-4
- ^ "Mexico 2050: The World's Fifth Largest Economy". 17 March 2010. Archived from the original on 19 August 2010. Retrieved 12 July 2013.
- ^ "World in 2050 – The BRICs and beyond: prospects, challenges and opportunities" (PDF). PwC Economics. Archived from the original (PDF) on 22 February 2013. Retrieved 17 July 2013.
- ^ a b c "Mexican Consumer Electronics Industry Second Largest Supplier of Electronics to the U.S – MEXICO CITY, Oct. 6, 2011/PRNewswire-USNewswire/". PR Newswire. 6 October 2011. Archived from the original on 15 December 2018. Retrieved 23 April 2014.
- ^ "Mexico tops U.S., Canadian car makers". Upi.com. 11 December 2008. Archived from the original on 31 August 2019. Retrieved 30 May 2010.
- ^ a b c Gereffi, G; Martínez, M (2005). "Mexico's Economic Transformation under NAFTA". In Crandall, R; Paz, G; Roett, R (eds.). Mexico's Democracy at Work: Political and Economic Dynamics. Lynne Reiner Publishers (published 30 September 2004). ISBN 978-1-58826-300-1.
- ^ Hufbauer, G.C.; Schott, J.J. (1 January 2005). "Chapter 6, The Automotive Sector" (PDF). NAFTA Revisited: Achievements and Challenges. Washington, D.C.: Institute for International Economics (published October 2005). pp. 1–78. ISBN 978-0-88132-334-4.
- ^ García, Daniela (7 September 2016). "Inauguran Kia Motors en Pesquería" [Kia Motors launched in Pesquería]. Milenio (in Spanish). Pesquería. Archived from the original on 4 June 2020. Retrieved 4 June 2020.
- ^ "Audi inaugura planta automotriz en Puebla" [Audi opens automotive plant in Puebla]. Autoexplora (in Spanish). 30 September 2016. Archived from the original on 27 September 2020. Retrieved 4 June 2020.
- ^ "Automaker Kia plans $1 bn assembly plant in Mexico". Mexico News.Net. 28 August 2014. Archived from the original on 3 September 2014. Retrieved 28 August 2014.
- ^ DINA Camiones Company. "History". Archived from the original on 13 May 2011. Retrieved 15 April 2009.
- ^ Jeremy Korzeniewski. "London 2008: Mastretta MXT will be Mexico's first homegrown car". Archived from the original on 20 February 2019. Retrieved 30 July 2008.
- ^ "Korea's Balance of Payments" (PDF). Archived from the original (PDF) on 1 May 2011. Retrieved 9 March 2011.
- ^ "Major Foreign Holders Of Treasury Securities". U.S. Department of the Treasury. Archived from the original on 23 November 2010. Retrieved 17 July 2013.
- ^ Thompson, Adam (20 June 2006). "Mexico, Economics: The US casts a long shadow". Financial Times. Archived from the original on 23 October 2012.
- ^ [8] Archived 11 May 2022 at the Wayback Machine "Personal Remittances Received, Mexico", World Bank accessed 11 May 2022
- ^ [9] Archived 11 May 2022 at the Wayback Machine "Latino Remittances from Mexico Soar". NBC News accessed 11 May 2022
- ^ [10] Archived 18 May 2022 at the Wayback Machine "Most of the $33 Billion in Remittances to Mexico Flow Via U.S. Govt. Banking Program", Judicial Watch, accessed 12 May 2022
- ^ "How much should you earn in Mexico to belong to the middle or upper class?". The Mazatlan Post. 11 April 2019. Archived from the original on 15 July 2019. Retrieved 15 July 2019.
- ^ Smith, Noah (26 August 2019). "Mexico Is Solidly Middle Class (No Matter What Trump Says)". Bloomberg. Archived from the original on 8 January 2024. Retrieved 27 September 2019.
- ^ "Human Development Report 2009" (PDF). United Nations Development Programme. United Nations. p. 118. Archived (PDF) from the original on 8 June 2020. Retrieved 4 June 2020.
- ^ "CONEVAL Informe 2011" (PDF). Archived from the original (PDF) on 21 October 2013. Retrieved 31 March 2012.
- ^ Gómez Mena, Carolina (10 August 2023). "Reducción de casi 9 millones de personas en pobreza entre 2020-2022: Coneval" [Decrease of nearly 9 million people in poverty between 2020-2022: Coneval]. La Jornada (in Spanish). Archived from the original on 12 December 2023. Retrieved 11 December 2023.
- ^ Moy, Valeria (15 August 2023). "Buenas y malas en la reducción de la pobreza" [Good and bad news regarding the decrease in poverty]. El Universal (in Spanish). Archived from the original on 12 December 2023. Retrieved 11 December 2023.
- ^ Soto, Dulce (25 September 2023). "Expertos y ONG dudan que pobreza en México haya disminuido como reportó Coneval" [Experts and NGO doubt that poverty in Mexico has decreased as Coneval reported]. Expansión Política (in Spanish). Archived from the original on 12 December 2023. Retrieved 11 December 2023.
- ^ Michael Blastland (31 July 2009). "Just what is poor?". BBC News. Retrieved 27 August 2019. The "economic distance" concept, and a level of income set at 60% of the median household income
- ^ "Under Pressure: The Squeezed Middle Class" (PDF). Paris: OECD Publishing. 2019. Archived (PDF) from the original on 1 July 2020. Retrieved 4 June 2020.
- ^ "Income inequality". Society at a Glance 2011: Social Indicators. OECD. 12 April 2011. ISBN 9789264098527. Archived from the original on 10 October 2017.
- ^ "Perspectivas OCDE: México; Reformas para el Cambio" (PDF). OECD. January 2012. pp. 35–36. Archived (PDF) from the original on 22 May 2012. Retrieved 17 July 2013.
- ^ "Goldman Sachs Paper No.153 Relevant Emerging Markets" (PDF). Archived from the original (PDF) on 31 March 2010. Retrieved 30 May 2010.
- ^ "Sobresale Nuevo León por su alto nivel de vida". El Norte (in Spanish). 2006. Archived from the original on 8 January 2024. Retrieved 22 January 2007.
- ^ Suárez, Karina (1 December 2023). "El salario mínimo en México aumentará un 20% en 2024" [The Mexican minimum wage will increase by 20% in 2024]. El País (in Spanish). Archived from the original on 8 January 2024. Retrieved 11 December 2023.
- ^ "Mexico – Telecoms Infrastructure, Operators, Regulations – Statistics and Analyses". Budde.com. 2019. Archived from the original on 15 July 2019. Retrieved 15 July 2019.
- ^ a b "Communications". CIA Factbook. Archived from the original on 26 January 2021. Retrieved 17 July 2013.
- ^ "Satmex. Linking the Americas". 15 September 2009. Archived from the original on 15 September 2009. Retrieved 17 July 2013.
- ^ Source: Arianespace (14 February 2002). "Mexican Operator Satmex Has Chosen Arianespace to Launch Its New Satmex 6 Satellite". Spaceref.com. Archived from the original on 11 March 2023. Retrieved 8 August 2011.
- ^ "Televisa Brings 2006 FIFA World Cup to Mexico in HD With Snell & Wilcox Kahuna SD/HD Production Switcher". Snellwilcox.com. Archived from the original on 14 December 2007. Retrieved 30 May 2010.
- ^ América Economia. "Top 500 Companies in Latin America" (Requires subscription). Retrieved 16 February 2007. [dead link]
- ^ "Fortune Global 500 2010: 64. Pemex". Fortune. Archived from the original on 10 April 2014. Retrieved 26 July 2010.
- ^ "FT Non-Public 150 – the full list". Financial Times. 14 December 2006. Archived from the original on 11 December 2022. Retrieved 26 July 2010.
- ^ Energy Information Administration. "Top World Oil Net Exporters and Producers". Archived from the original on 16 February 2007. Retrieved 16 February 2007.
- ^ "EIA". Eia.doe.gov. Archived from the original on 9 March 2006. Retrieved 30 October 2010.
- ^ Sener & GTZ 2006
- ^ "Perspectiva Del Mercado De La Energía Renovable En México" (PDF). Archived from the original (PDF) on 3 October 2008. Retrieved 30 October 2010.
- ^ a b SENER 2009b
- ^ Sonora Energy Group Hermosillo
- ^ Coerver, Don M.; Pasztor, Suzanne B.; Buffington, Robert (2004). Mexico: An Encyclopedia of Contemporary Culture and History. ABC-CLIO. p. 161. ISBN 978-1-57607-132-8. Archived from the original on 8 January 2024. Retrieved 20 December 2020.
- ^ Summerfield, Devine & Levi (1998), p. 285[full citation needed]
- ^ Summerfield, Devine & Levi (1998), p. 286[full citation needed]
- ^ Forest & Altbach (2006), p. 882[full citation needed]
- ^ Fortes & Lomnitz (1990), p. 18[full citation needed]
- ^ "The Nobel Prize in Chemistry 1995". Nobelprize.org. Nobel Foundation. Archived from the original on 26 December 2018. Retrieved 2 January 2009.
- ^ Thomson, Elizabeth A. (18 October 1995). "Molina wins Nobel Prize for ozone work". Massachusetts Institute of Technology. Archived from the original on 9 January 2014. Retrieved 2 January 2009.
- ^ Carramiñana, Alberto (2007). "Unravelling unidentified γ-ray sources with the large millimeter telescope". The Multi-Messenger Approach to High-Energy Gamma-Ray Sources. pp. 527–530. doi:10.1007/978-1-4020-6118-9_79. ISBN 978-1-4020-6117-2. Archived from the original on 8 January 2024. Retrieved 20 December 2020.
- ^ WIPO (6 May 2024). Global Innovation Index 2023, 15th Edition. World Intellectual Property Organization. doi:10.34667/tind.46596. ISBN 978-92-805-3432-0. Archived from the original on 22 October 2023. Retrieved 28 October 2023.
{{cite book}}:|website=ignored (help) - ^ "Global Innovation Index". INSEAD Knowledge. 28 October 2013. Archived from the original on 2 September 2021. Retrieved 2 September 2021.
- ^ Magalhães, Bianca dos Santos (2017). UNWTO Tourism Highlights. World Tourism Organization (UNWTO). doi:10.18111/9789284419029. ISBN 9789284419029. Archived from the original on 4 April 2023. Retrieved 4 March 2023.[page needed]
- ^ "Turismo de internación 2001–2005, Visitantes internacionales hacia México" (in Spanish). Secretaría de Turismo (SECTUR). 2006. Archived from the original on 10 June 2008. Retrieved 26 July 2008. pp. 5
- ^ "The Travel & Tourism Competitiveness Report 2017" (PDF). World Economic Forum. April 2017. Archived (PDF) from the original on 25 May 2017. Retrieved 16 October 2017.
- ^ "Cabo Fishing Information - Sport Fishing in Los Cabos". icabo.com. Archived from the original on 2 May 2013. Retrieved 23 April 2014.
- ^ Dallen J. Timothy, ed. (2019). Handbook of Globalisation and Tourism. Edward Elgar Publishing. p. 327. ISBN 9781786431295.
- ^ "CIA World Factbook". CIA. Archived from the original on 26 January 2021. Retrieved 20 December 2010.
- ^ a b "Infraestructura Carretera" (PDF). dgaf.sct.gob.mx. México: Secretaría de Comunicaciones y Transportes. Archived from the original (PDF) on 16 July 2007. Retrieved 13 January 2007.
- ^ Transporte, Instituto Mexicano del. "Red Nacional de Caminos". gob.mx (in Spanish). Archived from the original on 3 May 2023. Retrieved 6 July 2023.
- ^ "Infographic: Who Has The Best Roads?". Statista Daily Data. 19 October 2018. Archived from the original on 8 July 2023. Retrieved 6 July 2023.
- ^ a b "Mexico reviving travel by train". Azcentral.com. 6 January 2006. Retrieved 30 October 2010. [dead link]
- ^ "Bullet Train To Mexico City Looks To Be Back On Track ?". Guadalajara Reporter. 17 October 2003. Archived from the original on 30 April 2011. Retrieved 30 October 2010.
- ^ a b "Project for a Mexico City – Guadalajara High Speed Line. Rail transport engineering, public transport engineering". Systra. Archived from the original on 1 May 2011. Retrieved 30 October 2010.
- ^ "Slim to invest in Santa Cruz". The America's Intelligence Wire. 21 January 2005. Archived from the original on 18 January 2012.
- ^ "Mexico Real Estate In Yucatan to Benefit from New Bullet Train". Articlealley.com. 25 August 2010. Archived from the original on 27 July 2011. Retrieved 30 October 2010.
- ^ "Acerca del AICM. Posicionamiento del Aeropuerto Internacional de la Ciudad de México (AICM) con los 50 aeropuertos más importantes del mundo". AICM. Archived from the original on 31 May 2008. Retrieved 30 May 2010.
- ^ "Statistics Mexico City airport" (PDF). Mexico City International Airport. Archived from the original (PDF) on 14 January 2018. Retrieved 12 January 2018.
- ^ [11] [dead link] World Fact Book, Mexico. accessed 5 May 2022
- ^ "México cuenta con 123.5 millones de habitantes" [Mexico has 123.5 million inhabitants]. El Economista (in Spanish). Notimex. 10 July 2017. Archived from the original on 19 September 2017. Retrieved 4 June 2020.
- ^ a b "Spanish Language History". Today Translations. Archived from the original on 17 April 2005. Retrieved 1 October 2007.
- ^ "General Census of the Mexican Republic 1900". www.inegi.org.mx. National Institute of Statistics and Geography (INEGI). 28 October 1900. Archived from the original on 26 February 2023. Retrieved 6 June 2023.
- ^ "Population, total | Data". data.worldbank.org. 2022. Archived from the original on 6 June 2023. Retrieved 6 June 2023.
- ^ Knight, Alan. 1990. "Racism, Revolution and indigenismo: Mexico 1910–1940". Chapter 4 in The Idea of Race in Latin America, 1870–1940. Richard Graham (ed.) pp. 78–85
- ^ Wimmer, Andreas, 2002. Nationalist Exclusion and Ethnic Conflict: Shadows of Modernity, Cambridge University Press page 115
- ^ Hall Steckel, Richard; R. Haines, Michael (2000). A population history of North America. Cambridge University Press. p. 621. ISBN 978-0-521-49666-7. Archived from the original on 8 January 2024. Retrieved 17 June 2015.
- ^ "en el censo de 1930 el gobierno mexicano dejó de clasificar a la población del país en tres categorías raciales, blanco, mestizo e indígena, y adoptó una nueva clasificación étnica que distinguía a los hablantes de lenguas indígenas del resto de la población, es decir de los hablantes de español". Archived from the original on 23 August 2013.
- ^ "Al respecto no debe olvidarse que en estos países buena parte de las personas consideradas biológicamente blancas son mestizas en el aspecto cultural, el que aquí nos interesa (p. 196)" (PDF). Redalyc.org. 16 March 2005. Archived from the original (PDF) on 22 October 2013. Retrieved 27 June 2013.
- ^ Fuentes-Nieva, Ricardo (6 July 2017). "Ser blanco" [Being white]. El Universal (in Spanish). Archived from the original on 25 February 2021. Retrieved 20 December 2020.
- ^ Solís, Arturo (7 August 2018). "Comprobado con datos: en México te va mejor si eres blanco" [Proven with data: in Mexico you do better if you are white]. Forbes México (in Spanish). Archived from the original on 14 November 2020. Retrieved 20 December 2020.
- ^ Schwartz-Marín, Ernesto; Silva-Zolezzi, Irma (2010). ""The Map of the Mexican's Genome": Overlapping national identity, and population genomics". Identity in the Information Society. 3 (3): 489–514. doi:10.1007/s12394-010-0074-7. hdl:10871/33766.
- ^ R. Martínez & C. De La Torre (2008): "Racial Appearance And Income In Contemporary Mexico, pag 9 note 1" Archived 6 August 2021 at the Wayback Machine, Journal of Diversity Management, 2008, Retrieved 1 April 2021.
- ^ Navarrete Linares, Federico. "El mestizaje en Mexico" [The miscegenation in Mexico] (PDF) (in Spanish). Archived from the original (PDF) on 1 August 2017. Retrieved 31 July 2017.
- ^ Ruiz-Linares, Andrés; Adhikari, Kaustubh; Acuña-Alonzo, Victor; Quinto-Sanchez, Mirsha; Jaramillo, Claudia; Arias, William; Fuentes, Macarena; Pizarro, María; Everardo, Paola; de Avila, Francisco; Gómez-Valdés, Jorge; León-Mimila, Paola; Hunemeier, Tábita; Ramallo, Virginia; Silva de Cerqueira, Caio C.; Burley, Mari-Wyn; Konca, Esra; de Oliveira, Marcelo Zagonel; Veronez, Mauricio Roberto; Rubio-Codina, Marta; Attanasio, Orazio; Gibbon, Sahra; Ray, Nicolas; Gallo, Carla; Poletti, Giovanni; Rosique, Javier; Schuler-Faccini, Lavinia; Salzano, Francisco M.; Bortolini, Maria-Cátira; Canizales-Quinteros, Samuel; Rothhammer, Francisco; Bedoya, Gabriel; Balding, David; Gonzalez-José, Rolando (25 September 2014). "Admixture in Latin America: Geographic Structure, Phenotypic Diversity and Self-Perception of Ancestry Based on 7,342 Individuals". PLOS Genetics. 10 (9): e1004572. doi:10.1371/journal.pgen.1004572. PMC 4177621. PMID 25254375.
- ^ Spanish → Mexico at Ethnologue (18th ed., 2015) (subscription required)
- ^ Werner 2001, pp. 443, 444, 445.
- ^ INALI [Instituto Nacional de Lenguas Indígenas] (14 January 2008). "Catálogo de las lenguas indígenas nacionales: Variantes lingüísticas de México con sus autodenominaciones y referencias geoestadísticas" (PDF online facsimile). Diario Oficial de la Federación (in Spanish). 652 (9). Mexico City: 22–78 (first section), 1–96 (second section), 1–112 (third section). OCLC 46461036. Archived (PDF) from the original on 16 October 2011. Retrieved 22 July 2011.
- ^ a b c "Indigenous Languages in Mexico: Speakers Aged Three or Older". National Institute of Statistics and Geography. 2015. Archived from the original on 3 March 2016. Retrieved 11 September 2018.
- ^ "Ley General de Derechos Lingüísticos de los Pueblos Indígenas" (PDF) (in Spanish). 2003. Archived from the original (PDF) on 21 September 2013. Retrieved 3 August 2017.
- ^ "Model of Accreditation and Certification of Indigenous Languages" (PDF) (in Spanish). National Indigenous Languages Institute. October 2012. p. 7. Archived (PDF) from the original on 13 November 2018. Retrieved 11 September 2018.
- ^ "The Mennonite Old Colony Vision: Under siege in Mexico and the Canadian Connection" (PDF). Archived from the original (PDF) on 5 February 2007. Retrieved 11 September 2018.
- ^ Venetian (Mexico) at Ethnologue (18th ed., 2015) (subscription required)
- ^ "English in Mexico: An examination of policy, perceptions and influencing factors" (PDF). British Council. May 2015. Archived (PDF) from the original on 13 November 2018. Retrieved 11 September 2018.
- ^ Becerril, Isabel (27 April 2015). "En México sólo 5% de la población habla inglés: IMCO" (in Spanish). El Financiero. Archived from the original on 12 September 2018. Retrieved 11 September 2018.
- ^ "Une Langue Pour Apprendre" (PDF) (in French). Organisation internationale de la Francophonie. 6 September 2010. p. 132. Archived from the original (PDF) on 13 November 2018. Retrieved 11 September 2018.
- ^ "Cours de français" (in French). Ambassade de France à Mexico. 19 March 2013. Archived from the original on 19 August 2017. Retrieved 11 September 2018.
- ^ Simon-Clerc, Nathalie (2 November 2016). "Le Mexique, l'acteur qui monte dans la francophonie d'Amérique" (in French). L'Outarde Libérée. Archived from the original on 12 September 2018. Retrieved 11 September 2018.
- ^ a b c d e "Yearbook of Migration and Remittances: Mexico 2018" (PDF). BBVA Research. 2018. Archived (PDF) from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ a b c Gonzalez-Barrera, Ana (9 July 2021). "Before COVID-19, more Mexicans came to the U.S. than left for Mexico for the first time in years". Pew Research Center. Archived from the original on 5 April 2024. Retrieved 4 June 2024.
- ^ "Seminar: "Statistical Information of the Mexican Population Abroad"". en.www.inegi.org.mx. Archived from the original on 22 March 2024. Retrieved 4 June 2024.
- ^ "Mexican Migrants in the United States". Migration Policy Institute. 17 March 2016. Archived from the original on 3 July 2020. Retrieved 9 September 2018.
- ^ "Hispanic or Latino Origin by Specific Origin". U.S. Census Bureau. 2016. Archived from the original on 19 August 2018. Retrieved 9 September 2018.
- ^ Facts on Hispanics of Mexican origin in the United States, 2021 Archived 4 June 2024 at the Wayback Machine | Pew Research Center
- ^ "2011 National Household Survey". Statistics Canada. 8 May 2013. Archived from the original on 15 July 2017. Retrieved 9 September 2018.
- ^ "Number of Mexican emigrants worldwide by country of destination 2020". Statista. Archived from the original on 27 November 2023. Retrieved 4 June 2024.
- ^ a b c "Table 1: Total migrant stock at mid-year by origin and by major area, region, country or area of destination, 2017". United Nations Department of Economic and Social Affairs, Population Division. Archived from the original on 23 August 2018. Retrieved 9 September 2018.
- ^ "Principales resultados de la Encuesta Intercensal 2015 Estados Unidos Mexicanos" (PDF). INEGI. p. 1. Archived from the original (PDF) on 10 December 2015. Retrieved 9 September 2018.
- ^ "International Migration Outlook 2023 | Mexico". www.oecd-ilibrary.org. Retrieved 4 June 2024.
- ^ a b González, Alex; Ormerod. "A New Wave of Migration Is Changing Mexico". Americas Quarterly. Archived from the original on 4 June 2024. Retrieved 4 June 2024.
- ^ Smith, Dr. Claire M. (August 2010). "These are our Numbers: Civilian Americans Overseas and Voter Turnout" (PDF). OVF Research Newsletter. Overseas Vote Foundation. Archived from the original (PDF) on 24 October 2013. Retrieved 9 September 2018.
Previous research indicates that the number of U.S. Americans living in Mexico is around 1 million, with 600,000 of those living in Mexico City.
- ^ "Los árabes de México. Asimilación y herencia cultural" [The Arabs of Mexico: Assimilation and cultural heritage] (PDF) (in Spanish). December 2005. Archived (PDF) from the original on 27 March 2009. Retrieved 17 April 2010.
- ^ "Los Menonitas en México" [The Menonnites in Mexico]. Fundación UNAM. 28 August 2013. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "México atrae a españoles desempleados" [Mexico attracts unemployed Spaniards]. CNN. 24 April 2013. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "Crece 580% migración a México" [Increase of 580% in immigration to Mexico]. El Sol de México. 25 March 2018. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "Por la crisis, llegan a México más venezolanos expulsados" [Due to the crisis, more expelled Venezuelans arrive in Mexico]. Milenio. 5 May 2017. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "Una crisis migratoria en América del Sur: la salida de venezolanos pone a prueba la hospitalidad de países vecinos" [A migration crisis in South America: the departure of Venezuelans tests the hospitality of neighboring countries]. La Patilla. 19 July 2018. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "Japoneses hacen de Guanajuato su hogar" [Japanese make Guanajuato their home]. El Sol de México. 4 December 2017. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "Pesquería, el municipio de NL 'inundado' de coreanos" [Pesquería, the Nuevo León municipality 'flooded' with Koreans]. El Sol de México. 27 June 2018. Archived from the original on 10 September 2018. Retrieved 9 September 2018.
- ^ "Censo de Población y Vivienda 2020 - SCITEL" (in Spanish). INEGI. Retrieved 27 January 2021.
- ^ "Censo de Población y Vivienda 2020 – Cuestionario básico". INEGI. Archived from the original on 19 December 2023. Retrieved 18 May 2022.
- ^ "Main religion affiliations in Mexico". Statista. Archived from the original on 18 May 2023. Retrieved 19 May 2022.
- ^ Olvera, Graciela; Martínez, Armando (25 January 2021). "Catolicismo y otras religiones pierden creyentes en México". Milenio (in Spanish). Archived from the original on 30 March 2021. Retrieved 25 March 2021.
- ^ "The Largest Catholic Communities". Adherents.com. Archived from the original on 12 November 2007. Retrieved 10 November 2007.
- ^ "Church attendance". Study of worldwide rates of religiosity. University of Michigan. 1997. Archived from the original on 1 September 2006. Retrieved 3 January 2007.
- ^ "Our Lady of Guadalupe". Catholic Online. Archived from the original on 11 December 2018. Retrieved 24 October 2011.
- ^ "Cristianismos orientales: persecución, muerte, migración y cambio – Resonancias – Instituto de Investigaciones Sociales" Archived 21 October 2020 at the Wayback Machine, "UNAM", Mexico DF, 29 November 2019. Retrieved on 28 November 2020.
- ^ Primack, Karen (1998). Jews in places you never thought of. KTAV Publishing House, Inc. p. 305. ISBN 978-0-88125-608-6. Archived from the original on 8 January 2024. Retrieved 7 October 2020.
- ^ Jacobo Grinberg Zylberbaum (1989). Los chamanes de México (University of Texas ed.). Mexico City: UNAM School of Psychology. ISBN 9686022015. Archived from the original on 21 February 2024. Retrieved 19 August 2019.
- ^ Castells Ballarin, Pilar (June 2008). "La Santa Muerte y la cultura de los derechos humanos". LiminaR. 6 (1): 13–25. doi:10.29043/liminar.v6i1.263.
- ^ Soto Laveaga, Gabriela. "Bringing the Revolution to| Medical School: Social Service and a Rural Health Emphasis." Mexican Studies/Estudios Mexicanos vol. 29 (2) summer 2013, 397–427.
- ^ "Mexico – Health Care and Social Security". Countrystudies.us. Retrieved 30 May 2010.
- ^ a b "Health Care in Mexico". Expatforum.com. 8 August 2009. Retrieved 30 May 2010.
- ^ "Health Care Issues Mexico". Kwintessential.co.uk. Archived from the original on 13 August 2013. Retrieved 4 November 2009.
- ^ "Sistema Nacional de Información en Salud – Infraestructura". Sinais.salud.gob.mx. Archived from the original on 9 June 2010. Retrieved 30 May 2010.
- ^ "Mexico Literacy Rate 1980-2021". www.macrotrends.net.
- ^ a b "2019 Mexico Rankings". Top Universities. Retrieved 6 July 2023.
- ^ a b "University Rankings - Mexico 2023". www.scimagoir.com. Retrieved 6 July 2023.
- ^ a b "Mexico | Ranking Web of Universities: Webometrics ranks 30000 institutions". www.webometrics.info. Retrieved 6 July 2023.
- ^ "URAP - University Ranking by Academic Academic Performance". urapcenter.org. Retrieved 6 July 2023.
- ^ "Mexico - Health, Welfare, Poverty | Britannica". www.britannica.com. Retrieved 4 June 2024.
- ^ "Indigenismo | Indigenous Rights, Cultural Identity & Social Justice | Britannica". www.britannica.com. Retrieved 4 June 2024.
- ^ Vasconcelos, José (1997). La Raza Cósmica (The Cosmic Race). Didier T. Jaén (translator). The Johns Hopkins University Press. p. 160. ISBN 978-0-8018-5655-6.
- ^ Phelan, John Leddy (1 August 1956). "México y lo Mexicano". Hispanic American Historical Review. 36 (3): 309–318. doi:10.1215/00182168-36.3.309. JSTOR 2509215.
- ^ Katzew, Ilona. Casta Painting: Images of Race in Eighteenth-Century Mexico. New Haven: Yale University Press 2005
- ^ Widdiefield, Stacie G. The Embodiment of the National in Late Nineteenth-Century Mexican Painting. Tucson: University of Arizona Press 1996
- ^ Anreus, Robin Adèle Greeley, and Leonard Folgarait, eds. Mexican Muralism: A Critical History. Berkeley and Los Angeles: University of California Press 2012.
- ^ Lozano, Luis-Martin, ed. Frida Kahlo: The Complete Paintings. Taschen 2021.ISBN 9783836574204
- ^ Amadour, Ricky (28 April 2022). "Urs Fischer Spotlights Pluralistic Notions of Love". Frieze. No. 228. ISSN 0962-0672. Retrieved 1 January 2024.
- ^ Greet, Michele; Tarver, Gina McDaniel (8 March 2018). Art Museums of Latin America: Structuring Representation. Routledge. ISBN 978-1-351-77790-2.
- ^ "Museo Tamayo celebrates contemporary art in Mexico City - The Yucatan Times". 11 June 2023. Retrieved 1 January 2024.
- ^ Kinsella, Eileen (3 May 2018). "Mexico City's kurimanzutto Gallery Opens a New York Outpost With a Scrappy Ode to the Big Apple". Artnet News. Retrieved 1 January 2024.
- ^ Kinsella, Eileen (23 November 2020). "Latin American Galleries Missing Out on Miami Beach Have Banded Together to Form Their Own Version of Art Basel in Mexico City". Artnet News. Retrieved 1 January 2024.
- ^ Davison, Tamara (1 August 2018). "Gabriel Orozco: The pioneer of Mexico's modern art movement". Aztec Reports. Retrieved 1 January 2024.
- ^ UNESCO World Heritage Centre (29 June 2007). "UNESCO". Whc.unesco.org. Retrieved 17 August 2013.
- ^ "Arquitectura mexicana". www.arqhys.com. Archived from the original on 15 October 2017. Retrieved 15 January 2018.
- ^ Endicott, Katherine (14 October 2006). "The Mexican garden revisited". San Francisco Chronicle. Archived from the original on 19 September 2011. Retrieved 26 June 2009.
- ^ a b "El mole símbolo de la mexicanidad" (PDF). CONACULTA. Retrieved 27 September 2016.
- ^ University of Puget Sound. "History and influences of Mexican food". Archived from the original on 8 December 2011.
- ^ La Crónica de Hoy (20 September 2005). "Presentan en París candidatura de gastronomía mexicana". Archived from the original on 23 October 2012. Retrieved 19 January 2018.
- ^ esmas.com (25 November 2005). "Cocina mexicana, fuera de la UNESCO". Archived from the original on 23 October 2012.
- ^ Cocina, fiesta y cantos mexicanos reconocidos por UNESCO, El Universal (Mexico City) (newspaper), 16 November 2010, archived from the original on 24 October 2013, retrieved 19 January 2018
- ^ "Latina chef Daniela Soto-Innes is youngest to be named 'World's Best Female Chef'", NBC News, 26 April 2019, retrieved 12 July 2019
- ^ Curl, John (20 August 2009). "Aztec Poetry (1): Introduction". Aztecs at Mexicolore. Retrieved 14 July 2019.
- ^ a b González Echevarría, Roberto; Hill, Ruth, "Latin American literature", Encyclopaedia Britannica, retrieved 14 July 2019
- ^ Stevenson, Robert M. Music in Mexico: A Historical Survey. New York: Thomas Y. Crowell 1952
- ^ Russell, Craig. "Music: Mesoamerica through Seventeenth Century", Encyclopedia of Mexico, 976–980
- ^ Hess, Carol A. "Carlos Antonio de Padua Chávez y Ramírez", Encyclopedia of Mexico, 242–43
- ^ Zolov, Eric. "Counterculture", Encyclopedia of Mexico, 363–368
- ^ Zolov, Eric. Refried Elvis: The Rise of Mexican Counterculture. Berkeley and Los Angeles: University of California Press 1999.
- ^ "An Introduction to the Ballet Folklórico de México" ([12]). Accessed 15 May 2022.
- ^ [13] [dead link] World Fact Book, Mexico. accessed 4 May 2022
- ^ Hanna Rosin, "Life Lessons: How Soap Operas Can Change the World", The New Yorker, 5 June 2006, pp. 40–45.
- ^ Soto Laveaga, Gabriela, "'Let's become fewer': Soap operas, contraception, and nationalizing the Mexican family in an overpopulated world." Sexuality Research and Social Policy. September 2007, vol. 4, no. 3 pp. 19–33.
- ^ Dillingham, A.S. Oaxaca Resurgent: Indigeneity, Development, and Inequality in Twentieth-Century Mexico. Stanford: Stanford University Press 2021, 47–49, 69–70. ISBN 9781503627840
- ^ a b Baker, Shannon L. and William H. Beezley, "Sports", Encyclopedia of Mexico, 1370-1372
- ^ "2016 Binational Olympics". San Diego Metropolitan. December 2003. Archived from the original on 30 September 2007. Retrieved 7 October 2007.
- ^ "About CONCACAF". The Confederation of North, Central American and Caribbean Association Football (CONCACAF). Archived from the original on 6 October 2007. Retrieved 7 October 2007.
- ^ "México, una historia de éxito en la Serie Mundial de Ligas Menores" [Mexico, a history of success in the Minor League World Series], Medio Tiempo (in Spanish), 25 August 2010, retrieved 12 July 2019
- ^ "México es Campeón en el Mundial Sub-23 de beisbol" [Mexico is the World Baseball Champion in the Under-23 bracket], Medio Tiempo (in Spanish), 29 October 2018, retrieved 12 July 2019
- ^ "LOS TOROS EN MÉXICO" [Bullfighting in Mexico], Don Quijote (in Spanish), retrieved 11 July 2019
- ^ a b "Los mejores deportistas mexicanos de la historia" [The best Mexican athletes in history], Marca Claro (in Spanish), 12 October 2018, retrieved 11 July 2019
- ^ "Los medallistas que ha tenido el Box Olímpico mexicano" [The Mexican Olympic boxing medal winners], Caliente.mx (in Spanish), 15 August 2016, retrieved 11 July 2019
Further reading
- Anna, Timothy. Forging Mexico, 1821-1835. Lincoln: University of Nebraska Press 1998.
- Adams, Richard E.W. Prehispanic Mesoamerica. 3rd. ed. Norman: University of Oklahoma Press 2005.
- Beezley, William H., ed. A Companion to Mexican History and Culture. Blackwell 2011. ISBN 9781405190572
- Bulmer-Thomas, Victor, John H. Coatsworth, and Roberto Cortés Conde, eds. The Cambridge Economic History of Latin America. Vol. 1, The Colonial Era and the Short Nineteenth Century. Cambridge: Cambridge University Press 2006.
- Camp, Roderic Ai. Politics in Mexico: Democratic Consolidation or Decline? (Oxford University Press, 2014)
- Coerver, Don M., Suzanne B. Pasztor, and Robert M. Buffington. Mexico: An Encyclopedia of Contemporary Culture and History. Santa Barbara: ABCClio 2004. ISBN 1-57607-132-4
- Davis, Diane. Urban Leviathan: Mexico City in the Twentieth Century (Temple University Press, 2010)
- Hale, Charles A. The Transformation of Mexican Liberalism in Late Nineteenth-Century Mexico. Princeton: Princeton University Press 1989.
- Hamnett, Brian R. Roots of Insurgency: Mexican Regions 1750-1824. Cambridge: Cambridge University Press 1985.
- Kirkwood, Burton. The History of Mexico (Greenwood, 2000) online edition Archived 24 December 2009 at the Wayback Machine
- Knight, Alan. The Mexican Revolution. 2 vols. Cambridge: Cambridge University Press 1986.
- Krauze, Enrique (1998). Mexico: Biography of Power: A history of Modern Mexico 1810–1996. New York: Harper Perennial. p. 896. ISBN 978-0-06-092917-6.
- Levy, Santiago. Good intentions, bad outcomes: Social policy, informality, and economic growth in Mexico (Brookings Institution Press, 2010).
- Merrill, Tim and Ramón Miró. Mexico: a country study (Library of Congress. Federal Research Division, 1996) US government document; not copyright online free
- Meyer, Michael C.; Beezley, William H., eds. (2000). The Oxford History of Mexico. Oxford University Press. p. 736. ISBN 978-0-19-511228-3.
- Meyer, Michael C., William L. Sherman, and Susan M. Deeds. The Course of Mexican History (7th ed.) (Oxford University Press, 2002) online edition Archived 2 February 2011 at the Wayback Machine
- Rugeley, Terry. Epic Mexico: A History from Earliest Times. Norman: University of Oklahoma Press 2020. ISBN 9780806167077
- Van Young, Eric. Stormy Passage: Mexico from Colony to Republic, 1750-1850. Lanham MD: Rowman and Littlefield 2022. ISBN 9781442209015
- Vinson, Ben, III. Before Mestizaje: The Frontiers of Race and Caste in Colonial Mexico. New York: Cambridge University Press 2018.
- Werner, Michael S. ed. Encyclopedia of Mexico: History, Society & Culture (2 vol 1997) 1440pp online edition Archived 24 January 2010 at the Wayback Machine
- Werner, Michael S. (January 2001). Concise Encyclopedia of Mexico. Taylor & Francis. ISBN 978-1-57958-337-8.
External links
Government
- The Government of Mexico
- VisitMexico.com – Official tourism website (Archived 3 August 2022 at the Wayback Machine)
General information
- The World Factbook. Central Intelligence Agency. Mexico.
- U.S. Agency for International Development. Mexico.[permanent dead link]
- U.S.-Mexico foreign trade balance. Mexico.
- Mexico from BBC News
- Mexico at Encyclopædia Britannica
 Wikimedia Atlas of Mexico
Wikimedia Atlas of Mexico- Key Development Forecasts for Mexico from International Futures